El isomorfismo de Curry-Howard

Uno de los descubrimientos más impactantes en la lógica del siglo XX es el isomorfismo de Curry-Howard. También llamado la correspondencia de Curry-Howard o, como veremos inmediatamente, tipos como predicados.

Historia

Todo empezó cuando, en 1934, Haskell Curry se fijó en lo siguiente:

Si tengo una función f que toma un valor de tipo A y devuelve un valor de tipo B, su tipo lo escribiré como A -> B. Para indicar que f tiene ese tipo usaré los dos puntos f : A -> B y leeremos "f tiene tipo función de A a B". Escribiré los tipos en mayúsculas y los términos en minúscula. Para aplicar esa función a un término t arbitrario uso la siguiente regla de inferencia:

Si sé que f : A -> B y sé que t : A entonces puedo deducir que f(A) : B.

El golpe de genialidad de Curry consistió en quitar los términos y observar que los tipos solos conforman la regla de inferencia lógica del modus ponens.

Si sé que A implica a B y sé que A es cierto, entonces puedo deducir que B es cierto.

Tras años de trabajo, en 1958, Curry concluyó que no podía expresar la lógica proposicional clásica. Sólo una parte de ella llamada lógica intuicionista. En esta lógica no tenemos el principio del tercero excluido por lo que no podemos realizar demostraciones por reducción al absurdo.

Años más tarde, William Alvin Howard descubrió que no sólo se podía expresar la lógica proposicional intuicionista, sino un gran conjunto de lógicas intuicionistas incluidas las de primer orden y orden superior. Desde entonces se ha extendido aún más la correspondencia y se ha incluido la lógica clásica mediante el uso de continuaciones. De hecho, se han inventado lógicas gracias a la correspondencia.

Explicación

¿Pero cómo es posible que un tipo sea una proposición lógica? En todo caso un tipo es un conjunto de valores o de términos, pero ¿cómo expresar conjunciones o implicaciones? Aunque no lo parezca a primera vista, es relativamente fácil.

Por ejemplo, ¿qué significa cuando decimos 3 : int ? Que tres es un entero, sí. Pero también podemos decir que los enteros tienen algún habitante: existe un valor, el 3, que es un entero y por tanto los enteros no están vacíos. En este sentido el valor 3 sería la demostración de que los enteros están habitados. La proposición int significa "los enteros están habitados". Si nuestro lenguaje de programación no tuviera enteros, int sería falso. Si los tiene, int es cierto.

Entonces, los términos son, por un lado, valores de un tipo y, por otro, demostraciones de que ese tipo no está vacío. Que un tipo no esté vacío significa que, visto como proposición, tiene una demostración y por tanto es cierto en nuestro sistema o lenguaje de programación.

Seguimos: ¿Cómo demuestra una función una implicación? Viendo la regla modus ponens de arriba, la demostración de que B está habitado es f(t) así que lo que hace una función f es, dada una demostración t,  construye otra f(t). O como siempre se ha entendido, dado un valor devuelve otro. Por esta razón demuestra la implicación: dame una demostración de A que te doy otra de B. Si A es cierto, entonces B también.

Hasta ahora tengo predicados constantes como int e implicaciones como A->B. Introduciremos la conjunción A & B. Desde el punto de vista lógico si A & B es cierto es por que A es cierto y B es cierto. Si me pongo a trabajar con las demostraciones necesito la demostración de A y la demostración de B para tener la demostración de A & B. Llamemos a estas demostraciones a : A y b : B. Entonces, un término que agrupa ambas demostraciones es un par (a, b). Por tanto, el tipo conjunción no es más que el tipo de los pares (a, b) : A & B más usualmente llamado producto cartesiano.

De esta forma se pueden obtener todas las conectivas en gran cantidad de lógicas distintas y, lo que es más importante, se estandariza la forma de demostrar las proposiciones en dichas lógicas: Los programas son esas demostraciones.

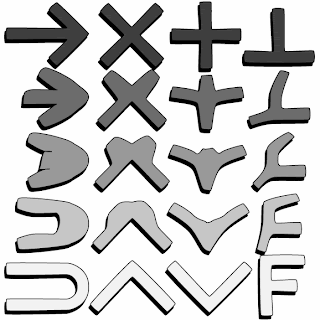Portada de las actas del congreso LICS'90, humorísticamente titulada el homeomorfismo de Curry-Howard. Los constructores de tipos (arriba) se transforman en las conectivas lógicas (abajo) de forma continua.

  

En acción

Para finalizar vamos a demostrar, usando programas como prueba, que A -> B -> C es lógicamente equivalente a (A & B) -> C. Para esto primero demostraremos ( (A & B) -> C) -> (A -> B -> C) y luego (A -> B -> C) -> ( (A & B) -> C).

λ f. (λ x. λ y. f (x, y) ) : ( (A & B) -> C) -> (A -> B -> C)
λ f. λ x. f (primero x) (segundo x) :  (A -> B -> C) -> ( (A & B) -> C)

Sólo hay que hacer notar que hemos usado las proyecciones de un par: primero (p, q) se evalúa a p y segundo (p, q) se evalúa a q. El resto de la demostración es obvia en el sentido de que el programa que proporciono tiene ese tipo que digo. Para comprobar eso harían falta ciertas reglas de inferencia, pero eso será para otro día.