Patrón decorador

Los patrones de diseño no son más que una manera conocida de resolver problemas. Incluso sin saber lo que son, es probable que cualquier programador los haya usado sin querer. Esto es así porque muchas veces son la solución más lógica y no dependen del lenguaje de programación que se use.

El patrón decorador se basa en el siguiente problema. Tengo una clase C y por alguna razón no puedo o no quiero tocarla, pero tendría que hacer algo que no hace. Es más, esta nueva funcionalidad ni siquiera necesita que modifiquemos su interfaz I (por lo que los usuarios de la clase ni se van a enterar que estoy modificando la funcionalidad por debajo).

La solución que propone el patrón decorador es crear otra clase D que implemente esta interfaz y que envuelva a la clase C. Cuando ejecutamos los miembros del interfaz de D, hacemos lo que tengamos que hacer como si fuéramos la clase C y, si fuera necesario, usamos la clase C que envolvemos. Es decir, suplantamos la clase C.

Ya está. Fácil, ¿no? Bueno, podemos refinar porque aún tenemos algunos problemillas. Si quiero agregar varias funcionalidades a C tendría que hacer una clase D1, D2..., pero también la que combina ambas cosas D12 (Imaginemos que C es un texto y las D son el tipo de letra. Entonces D1 sería "negrita", D2 sería "cursiva" y D12 "negrita y cursiva"). Si tuviera D1, D2, D3, D4... las combinaciones serían muchas. Es lo que se denomina una explosión exponencial.

Afortunadamente, la clase D puede envolver en vez de una clase C, una clase de interfaz I. Esto incluye otras clases D. En este caso, si escribo que D envuelve a C así D(C), la modificación D12 sería D1(D2(C)). Esto me evita tener que escribir clases compuestas D12, D24, etc y evito la explosión exponencial.

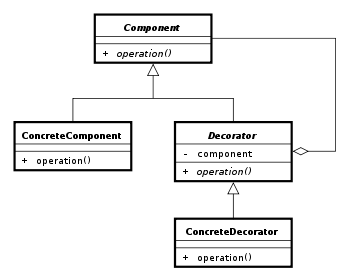
Por último, y para seguir la ley DRY, es conveniente que todas las clases D1, D2... deriven de una clase D común de "envoltura básica". Esto nos lleva al esquema usual del patrón decorador tal y como viene en la Wikipedia.

Donde

• "Component" es la interfaz común I.
• "ConcreteComponent" es la clase C que queremos modificar pero no tocar.
• "Decorator" es la clase base D de otros decoradores D1, D2... Esta clase lo único que hace es contener (envolver) un objeto de interfaz I.
• "ConcreteDecorator" son las clases D1, D2... que tengamos que implementen la nueva funcionalidad.

A vueltas con los rangos

Parece natural que, dado que una gran cantidad de algoritmos trabajan sobre una serie de datos, se realice una abstracción y lleguemos a la idea de rangos. Donde un rangos es una serie de datos.

Pero en la infomática seria las cosas no son tan fáciles y hay que definir la interfaz que tiene ese concepto. Es decir, qué operaciones se pueden realizar sobre los rangos y qué efecto tienen esas operaciones. Recientemente, en la BoostCon 2009, Alexandrescu dio una charla sobre las que él cree que serían esas operaciones básicas. Las transparencias de la charla están aquí y la interfaz que propone para los rangos (de entrada) es esta:

template struct InputRange {
bool empty() const;
void popFront();
T& front() const;
};

Esta simplicidad, y el hecho de que estén ya muy arraigados los iteradores, ha levantado una gran polvareda en la lista de desarrolladores de Boost. Rápidamente han salido detractores y defensores.

Particularmente, me parece una buena idea. Es otra abstracción y parece realmente versátil. Para algunas cosas valdrá y para otras tendrás que bajar al nivel de iteradores. Como siempre ha pasado en computación (y por eso aún hoy en día se usa el ensamblador.)

Con valor, como debe ser.

Leyendo InformIT me entero que el comité de estandarización del C++ ha rechazado los conceptos explícitos. Una pieza fundamental del nuevo estándar C++0x.

Un concepto implícito es una interfaz que no hace falta declararlo cuando se crea un tipo. Basta con que el tipo tenga las operaciones adecuadas para que cumpla el concepto. Así que si tengo un concepto "sumable" que requiera tener definido "operator+", tanto una clase que lo implemente como los enteros o los flotantes son "sumables". En teoría de tipos a esto se le llama "duck typing".

Cuando se introducen los conceptos en el lenguaje de forma sintáctica lo que tenemos son conceptos explícitos. Es decir, o digo que un entero es "sumable" o no puedo usarlo como "sumable". Esto tiene sus ventajas y sus inconvenientes. Por ejemplo, que sea "sumable" puede tener asociada la semántica de la suma pero un "operator+" podría no ser una suma. En ese caso sí que me interesa separar lo que es "sumable" de lo que parece "sumable". Por otra parte, ¿para qué tener que decir que es sumable?... si es que se ve. Debido a esto el comité de estandarización añadió los conceptos automáticos que no es más que los conceptos implícitos antes mencionados.

Se complica la cosa, ¿verdad?

Lo que realmente ocurre es que introducir algo explícito cuando ya existe eso mismo implícito no es buena idea si no es realmente necesario. Las necesidades que se proponían eran varias:

• Mejorar la notificación de los errores en los templates.
• Añadir semántica a los conceptos implícitos (mediante axiomas)
• Otras más que no llego a comprender o recordar.

Bueno. Creo que la primera necesidad es responsabilidad del compilador. El compilador debe acercar los errores al usuario y no vomitar la pila de argumentos de template. La segunda no es tampoco una necesidad muy necesaria ya que día a día los programadores usan identificadores para describir la semántica y no hay nada que les impida usar la función inadecuada en el momento inoportuno. Aún así, programan.

Así que bien visto, a pesar de estar tirando varios años de trabajo a la basura... ¡KISS!.

Conmutando matrices

Casi siempre que me encontraba con un producto matricial de varias matrices, tipo ABC, y tenía que sacar la matriz del centro (por ejemplo, era la incógnita) llegaba a la torpe conclusión de que no se podía. Iluso de mí. He descubierto un nuevo mundo matricial ya que si bien no se puede hacer ABC=BAC, sí que se puede hacer algo como ABC=B'A'C donde B' y A' son matrices inteligentemente construídas.

La siguiente ecuación resume el truco.

Obviamente queda la cosa mucho más fea y engorrosa, pero puedes continuar. Leyendo sobre cómo representar estas matrices de forma más compacta me he encontrado con una serie de productos matriciales extraños como:

• El producto de Kronecker
• El producto de Hadamard
• El producto de Tracy-Singh
• El producto de Khatri-Rao

Interesante tema, pero tan poco tiempo para dedicarle.

De circuitos y códigos

Recientemente estoy liado con la generación de señales de audio. Hay varios sistemas y la mayoría de ellos consisten en traducir un circuito a una serie de instrucciones de código. Los circuitos pueden ser vistos como grafos dirigidos donde cada nodo realiza una serie de tareas obteniendo la información de los arcos que le llegan y devolviendo la información procesada por los arcos que salen de él. Para simplificar las ideas me ceñiré a los grafos dirigidos acíclicos (conocidos por sus siglas en inglés DAG).

Ahora bien, ¿cómo convertir el DAG en una serie de instrucciones? Para empezar (y dado que no tenemos ciclos) podemos ordenar el DAG mediante su orden topológico. Luego tendremos que preguntarnos sobre la naturaleza de las señales que se conectan.
En CSOUND, las señales son o bien arreglos de flotantes o bien números flotantes sueltos. En esta plataforma se combinan ambos conceptos haciendo que un número flotante sea un arreglo de longitud unitaria. Esto hace que la estructura sea muy simple.

• Cada nodo tiene punteros a los trozos de memoria donde están sus entradas.
• Cada nodo tiene punteros a los trozos de memoria donde poner sus salidas.
• Se ejecutan los nodos en el orden topológico y ellos procesan los datos.

Ahora bien, debido a que el nodo no contiene la memoria de esas señales de entrada o salida, el sistema debe preocuparse en reservarlo y hacer que esos punteros apunten donde tienen que apuntar. Otra desventaja es que no hay control de flujo. Siempre hay que procesar las señales, aunque estas no hayan sido modificadas.
En Reaktor se soluciona esta desventaja a costa de tener que calcular el orden topológico cada vez que se quiera modificar o leer una señal. La estructura es bastante más compleja.

• Los nodos no saben por donde les llegan las señales, pero deben responder a los eventos que las modifiquen (venga de donde venga)
• Los nodos no saben dónde hay que enviar los resultados de su procesamiento. Es decir, que deben almacenarlo internamente hasta que se lo pidan.
• Los nodos se ejecutan bajo demanda mediante una búsqueda en profundidad. Esta búsqueda es equivalente a calcular el orden topológico aunque sólo para los nodos que lo requieran.
• Un nodo que quiera modificar un evento ha de comunicárselo al sistema y el sistema ya decidirá qué hacer con el evento.
• Un nodo que requiera datos para procesar ha de comunicárselo al sistema y el sistema ya decidirá de dónde sacarlos.

Como se observa, el sistema tiene muchas más responsabilidades en este segundo caso. Lo que significa que va a tener más estructuras auxiliares y va a usar algoritmos más complejos para hacer funcionar el circuito. A cambio, el proceso se realiza únicamente cuando se necesita y no continuamente.
Finalmente, se me ocurre otro sistema en el cual cada señal lleva asociado un flag que indica si ha sido modificada o no. Esto sería un punto intermedio entre los extremos anteriores, aunque tiene trampa ya que el nodo debe utilizar estos flags coherentemente volcando parte de la complejidad en los nodos. Esto último no es recomendable puesto que hay muchos nodos mientras que sólo hay un único sistema.
Por ahora, creo que voy a seguir por la senda de Reaktor.

Máquinas virtuales e instrucciones

Una máquina virtual es un procesador que se emula por software. Si la máquina virtual está pensada para ofrecer todas las prestaciones de un sistema real, se llama máquina virtual de sistema. Si es una abstracción para que algún proceso funcione, se llama máquina virtual de proceso. (Ver la Wiki).

Una máquina virtual puede ser una implementación de una máquina ideal que no exista. Es más, podemos inventarnos la máquina virtual que necesitemos para resolver un problema específico. Inventar las instrucciones de la máquina y definir su comportamiento es una de las partes más emocionantes de la creación de máquinas virtuales propias.

Personalmente he tratado con un tipo de máquinas virtuales que se denominan máquinas de pila. Sin embargo, hoy en día estoy con otro tipo llamadas máquinas de registro. Las primeras me parecen mucho más fáciles, pero he de reconocer que la comparación hecha en la Wikipedia deja claro que las segundas son mucho más rápidas. También hay un tercer tipo por lo que la lista completa sería:

• Máquinas de pila. Instrucciones sin argumentos del tipo PUSH, POP, ADD, SUB, etc.
• Máquinas de registro. Instrucciones con argumentos de origen y destino tipo ADD x,y; SUB x,y; etc.  Algunos juegos de instrucciones tienen también tres argumentos como MUL x, y, z;
• Máquinas de acumulador. Instrucciones con argumento de origen únicamente. El destino es un registro especial que es el acumulador. Serían cosas como ADD x; SUB x; etc.

Esta clasificación también se puede extender a máquinas reales, aunque sea muy difícil encontrar un microprocesador que sea exclusivamente de un tipo. Por ejemplo, la arquitectura i386 tiene instrucciones de pila (como FSUB), instrucciones de acumulador (como STOS) e instrucciones de registro de dos (como ADD) y de tres (como IMUL) argumentos.

La semántica perdida

Después de echarle un vistazo a la Wikipedia en su página sobre las semánticas formales, me queda la duda de otro tipo de semántica que no aparece. Quizás no se considere semántica, quizás nadie la haya visto como una semántica.

Si no me equivoco, la semántica operacional lo que hace es emular una máquina virtual que va evolucionando conforme el programa se ejecuta. La semántica denotacional le da un valor a cada elemento del lenguaje de forma que establece relaciones matemáticas entre ellos. Finalmente, la semántica axiomática establece asertos y valores de verdad que cada instrucción cumple, forma en la que se define el funcionamiento del programa.

Ahora bien, si ya tenemos un lenguaje con una semántica conocida, podríamos dar la semántica de otro lenguaje transformándolo en el lenguaje de semántica conocida.

Por ejemplo, si se introduce la sentencia

a += b

La semántica se podría especificar diciendo que la sentencia anterior es igual a

a = a + b

Claro que podría ser que esto ya fuera una de las semánticas de antes, la verdad, no lo sé.