¿Secuencial o Paralelo?

Este es un resumen de la charla de Guy Steele sobre paralelismo en Strange Loop.

SECUENCIAL	PARALELO
Se ejecuta un código A, luego se usa el resultado de A en otro código B.	Se ejecutan los códigos A y B independientemente. Luego se mezclan los resultados.
Reusa el espacio. Sólo hay que almacenar un resultado.	Usa espacio extra para desacoplar los cálculos.
Procesa una cosa cada vez y va acumulando resultados.	Descompone y mezcla resultados. Divide y vencerás.
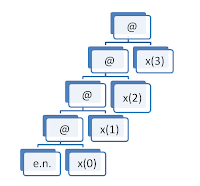
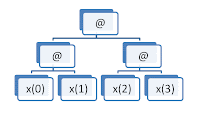
Requiere iniciar el acumulador con el elemento neutro de la operación. acc=elem_neutro; for(i=0; i<n; ++i)    acc=acc @  x[i]	Requiere asociatividad en la operación para ir mezclando resultados. No se puede procesar en paralelo: [$$ x_0 \star (x_1 \star (... )) $$]
Se basa en trucos para optimizar. Reordenación de instrucciones. Desplegado de bucles. Reutilización de registros. Ejecución especulativa. Predicción de saltos. etc.	Se basa en propiedades algebraicas para optimizar. Asociativa: La forma de agrupar operaciones no importa. Conmutativa: El orden de los operandos no importa. Idempotente: Las repeticiones no importan. Identidad: El elemento neutro puede ser ignorado. Cero: El resto de elementos puede ser ignorado.

Así que hay que hacer que el programador deje de pensar en acumuladores y pase a pensar en propiedades algebraicas. Es decir, usar catamorfismos en vez de bucles. Los catamorfismos no son más que funciones que toman una estructura de datos y devuelven un valor a partir de ella con la propiedad de que son morfismos. En el caso de sumar una lista de números sería algo así como convertir la concatenación en suma.

[$$ f( [ 3, 5 ] .. [4, 7] ) = f( [3,5] ) + f( [4, 7] ) $$]

Esto significa a su vez que hay que buscar una operación con las propiedades algebraicas que deseemos (o podamos obtener), lo cual puede llevar a comprender más profundamente el problema.

La especificación del catamorfismo es similar al uso de sumatorios en matemáticas. No se especifica el orden de la suma, sólo que hay que sumar los elementos.

[$$ \sum_{i=1}^{n} {x_i} $$]

En programación esto se tendría que hacer usando funciones de alto nivel como fold pero asumiendo la asociatividad.

fold_assoc( suma, [3, 5, 4, 7] )

Así el compilador podría optimizar usando paralelismo sin que el programador tuviera que luchar con sincronizaciones y demás.