martes, 22 de marzo de 2011
Reunión del C++ Standards Committee en Madrid
Es la primera vez en la historia que el comité de estandarización del C++ se reúne en España. Durante unos días, del 21 al 26 de marzo de 2011, estarán en tierras hispanas. En teoría, pero sólo en teoría, las reuniones son públicas. Por si os queréis animar, toda la información está aquí.
miércoles, 16 de marzo de 2011
Mónadas en un plis-plás
Como no hay blog de informática teórica que se precie sin un tutorial de mónadas, y aprovechando que Milewski está dedicándole unos posts a esto, voy a explicar cómo entendí lo de las mónadas (si es que lo entendí, claro).
De los efectos secundarios y de cómo evitarlos
Supongamos esta función.
int f(int x)
{
a=x+2;
return x*3;
}
Realmente, está haciendo dos cosas: retornar el triple y asignar el argumento más dos a una variable externa “a”. Esta segunda acción es lo que se llama un efecto secundario porque modifica el estado global del programa. En este caso, el valor de “a”.
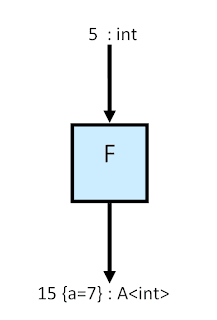
Muchas veces no es conveniente tener efectos secundarios: se simplifica la concurrencia, se permite la transparencia referencial, se permiten más optimizaciones, facilita la comprensión del programa, etc. Si queremos evitar que la función “f” tenga efectos secundarios la única solución es forzar a que éstos sean devueltos también por el retorno. Llamaremos a esta nueva función “F” para distinguirla de la original “f” con efectos secundarios.
El problema ahora es que tenemos que devolver dos tipos. Además, no hemos dicho nada de que la función “f” pueda hacer más de una asignación. Tampoco hemos hablado de cómo cambia este nuevo retorno el estado global. Lo mejor es abstraernos de todos estos detalles y decir que “F” devuelve asignaciones y un entero. Inventaremos el tipo “A<int>” para eso usando un constructor de tipos "A".
Así que “F” vuelve a ser una función normal y corriente con un tipo a devolver exótico que engloba tanto el retorno normal (el entero) como los efectos secundarios (las asignaciones).
¡Pero hemos perdido una operación fundamental en la programación! ¿Cómo hacemos composiciones? ¿Cómo hacemos cosas como “f(f(5))”? Ahora que los tipos no coinciden, ¡no es posible escribir “F(F(5))”!
La solución pasa por hacer explícita la aplicación. ¿Pero qué es una aplicación explícita?
De la aplicación explícita y las restricciones que la composición le impone
En esta sección sólo hablaremos de cosas conocidas: funciones puras sin efectos secundarios. Llamaremos “g” y “h” a estas funciones puras. Nos olvidaremos por ahora del tipo “A<int>” y de las funciones “f” y “F” con efectos secundarios.
La aplicación explícita es sencillamente escribir “apply(x, g)” en vez de escribir “g(x)”.
Es únicamente un cambio en la notación, pero nos permite estudiar las propiedades de “apply” y realizar cosas tan potentes como la defuncionalización (de la que no hablaremos aquí). En concreto, para que “apply” sea coherente con la composición, debe mantener sus dos propiedades: elemento neutro y asociativa.
Para el elemento neutro hemos de introducir una función identidad. La llamaremos “id” y devuelve su argumento sin hacer nada de nada.
int id(int v) {return v;} //Función identidad de los enteros
Obviamente, componer esta función no debe hacer nada.
apply(x, id) == x
apply(id(x), g) == g(x)
Para la asociativa introduciremos una función compuesta “h” que aplique consecutivamente dos funciones “g1” y “g2”. En notación matemática escribiríamos [$h=g_2 \circ g_1$].
int h(int v) { return apply(g1(v), g2); }
Entonces, aplicar esta función compuesta “h” es igual que aplicar consecutivamente “g1” y “g2”.
apply(v, h) == apply(apply(v, g1), g2)
Con esto estamos seguros de que “apply” se comporta correctamente para la composición y podemos volver a pensar cómo solucionar el problema de la composición de la función “F”.
Nota: La propiedad asociativa aquí expuesta no parece ser la propiedad asociativa de toda la vida, pero si usamos “@” como operador infijo para el “apply” y la composición, entonces la propiedad queda algo así como “v@(g1@g2) = (v@g1)@g2” lo cual sí que se parece ya a la propiedad asociativa usual.
De la mezcla de efectos secundarios con aplicaciones explícitas
Lo interesante de hacer explícita la aplicación es que podemos adaptar el tipo de la misma a nuestros requisitos. Llamaremos “bind” a la aplicación con el tipo “A<int>” sobre funciones de tipo “int -> A<int>”, para no confundirla con “apply” que funciona sobre “int” y funciones “int -> int” únicamente.
apply: int -> (int->int) -> int
bind: A<int> -> (int -> A<int> ) -> A<int>
El truco está en que “bind(xx, F)” toma los efectos secundarios de “xx” y los mezcla con los efectos secundarios del resultado de “F” para luego devolverlos en su resultado.
Pero queda el asunto de la composición que nos forzó a introducir el “bind”: debe cumplir exactamente las mismas propiedades que “apply”.
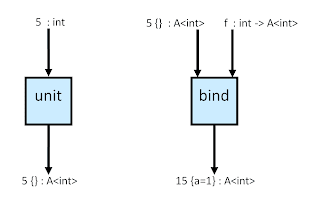
La única salvedad es que “id” no debe ser la función identidad de los enteros. Tenemos que mantener el tipo “int -> A<int>” en las funciones. Así que se ha de convertir en una función que toma un entero y devuelve un “A<int>” de la manera más neutra posible. Es decir, sin efectos secundarios. También vamos a cambiar el nombre de esta función para no confundirla con la “id” original y la vamos a llamar “unit”.
Pues bien. Estas tres cosas son una mónada:
De los lugares en los que habitan las mónadas
La parquedad de los requisitos de las mónadas hace que aparezcan por todos los lados y no únicamente como modelo de efectos secundarios. Son en general un modelo de computación (ver ejemplo 1.1 en el articulo original de Moggi para una lista de cosas que puede modelar una mónada).
Por ejemplo, los punteros con NULL se usan generalmente como mónadas. El constructor de tipo está claro que es el de los punteros. De “int” pasamos a “int*”. La función “unit” es simplemente obtener la dirección de un entero.
int a;
int* p=&a; // p=unit(a)
La función “bind” consiste en comprobar que el puntero no es NULL.
return p==NULL ? NULL : p->OperaYDevuelvePuntero() ;
// return bind(p, OperaYDevuelvePuntero);
Es fácil comprobar las propiedades correspondientes con estas operaciones, pero aún hay más. Cualquier colección iterable es una mónada. Sí, así a lo bestia: vectores, conjuntos, listas, mapas, tablas hash, etc. Todos son mónadas. El constructor de tipo es el de la colección que queramos. Por ejemplo, “vector<int>”.
La función “unit” es bien sencilla: la colección con un único elemento.
vector<int> v;
v.push_back(3);
// v=unit(3)
La función “bind” es equivalente a iterar y mezclar.
vector<int> r;
foreach (x in v) r.append(Procesa(x));
// r=bind(v, Procesa)
Ojo que “Procesa” devuelve un vector y “append” mezcla vectores. Si “Procesa” fuera obtener la lista de divisores, entonces
bind([1, 6, 21], Procesa) = [1, 1, 2, 3, 6, 1, 3, 7, 21]
Esta propiedad del “bind” de separar, iterar y combinar es la que le da tanta utilidad. De hecho, debido a esto, “Procesa” también serviría para filtrar, transformar, unir y casi cualquier otra operación que se quiera realizar con la colección. Lo que no quita para que también la colección tenga sus operaciones propias no monádicas.
Pero con todo esto habría ya material para otra entrega en la que tendríamos que hablar de comprensiones monádicas, la notación “do” y empezar a usar muchas funciones anónimas.
De los efectos secundarios y de cómo evitarlos
Supongamos esta función.
int f(int x)
{
a=x+2;
return x*3;
}
Realmente, está haciendo dos cosas: retornar el triple y asignar el argumento más dos a una variable externa “a”. Esta segunda acción es lo que se llama un efecto secundario porque modifica el estado global del programa. En este caso, el valor de “a”.
Muchas veces no es conveniente tener efectos secundarios: se simplifica la concurrencia, se permite la transparencia referencial, se permiten más optimizaciones, facilita la comprensión del programa, etc. Si queremos evitar que la función “f” tenga efectos secundarios la única solución es forzar a que éstos sean devueltos también por el retorno. Llamaremos a esta nueva función “F” para distinguirla de la original “f” con efectos secundarios.
El problema ahora es que tenemos que devolver dos tipos. Además, no hemos dicho nada de que la función “f” pueda hacer más de una asignación. Tampoco hemos hablado de cómo cambia este nuevo retorno el estado global. Lo mejor es abstraernos de todos estos detalles y decir que “F” devuelve asignaciones y un entero. Inventaremos el tipo “A<int>” para eso usando un constructor de tipos "A".
Así que “F” vuelve a ser una función normal y corriente con un tipo a devolver exótico que engloba tanto el retorno normal (el entero) como los efectos secundarios (las asignaciones).
¡Pero hemos perdido una operación fundamental en la programación! ¿Cómo hacemos composiciones? ¿Cómo hacemos cosas como “f(f(5))”? Ahora que los tipos no coinciden, ¡no es posible escribir “F(F(5))”!
La solución pasa por hacer explícita la aplicación. ¿Pero qué es una aplicación explícita?
De la aplicación explícita y las restricciones que la composición le impone
En esta sección sólo hablaremos de cosas conocidas: funciones puras sin efectos secundarios. Llamaremos “g” y “h” a estas funciones puras. Nos olvidaremos por ahora del tipo “A<int>” y de las funciones “f” y “F” con efectos secundarios.
La aplicación explícita es sencillamente escribir “apply(x, g)” en vez de escribir “g(x)”.
Es únicamente un cambio en la notación, pero nos permite estudiar las propiedades de “apply” y realizar cosas tan potentes como la defuncionalización (de la que no hablaremos aquí). En concreto, para que “apply” sea coherente con la composición, debe mantener sus dos propiedades: elemento neutro y asociativa.
Para el elemento neutro hemos de introducir una función identidad. La llamaremos “id” y devuelve su argumento sin hacer nada de nada.
int id(int v) {return v;} //Función identidad de los enteros
Obviamente, componer esta función no debe hacer nada.
apply(x, id) == x
apply(id(x), g) == g(x)
Para la asociativa introduciremos una función compuesta “h” que aplique consecutivamente dos funciones “g1” y “g2”. En notación matemática escribiríamos [$h=g_2 \circ g_1$].
int h(int v) { return apply(g1(v), g2); }
Entonces, aplicar esta función compuesta “h” es igual que aplicar consecutivamente “g1” y “g2”.
apply(v, h) == apply(apply(v, g1), g2)
Con esto estamos seguros de que “apply” se comporta correctamente para la composición y podemos volver a pensar cómo solucionar el problema de la composición de la función “F”.
Nota: La propiedad asociativa aquí expuesta no parece ser la propiedad asociativa de toda la vida, pero si usamos “@” como operador infijo para el “apply” y la composición, entonces la propiedad queda algo así como “v@(g1@g2) = (v@g1)@g2” lo cual sí que se parece ya a la propiedad asociativa usual.
De la mezcla de efectos secundarios con aplicaciones explícitas
Lo interesante de hacer explícita la aplicación es que podemos adaptar el tipo de la misma a nuestros requisitos. Llamaremos “bind” a la aplicación con el tipo “A<int>” sobre funciones de tipo “int -> A<int>”, para no confundirla con “apply” que funciona sobre “int” y funciones “int -> int” únicamente.
apply: int -> (int->int) -> int
bind: A<int> -> (int -> A<int> ) -> A<int>
El truco está en que “bind(xx, F)” toma los efectos secundarios de “xx” y los mezcla con los efectos secundarios del resultado de “F” para luego devolverlos en su resultado.
Pero queda el asunto de la composición que nos forzó a introducir el “bind”: debe cumplir exactamente las mismas propiedades que “apply”.
La única salvedad es que “id” no debe ser la función identidad de los enteros. Tenemos que mantener el tipo “int -> A<int>” en las funciones. Así que se ha de convertir en una función que toma un entero y devuelve un “A<int>” de la manera más neutra posible. Es decir, sin efectos secundarios. También vamos a cambiar el nombre de esta función para no confundirla con la “id” original y la vamos a llamar “unit”.
Pues bien. Estas tres cosas son una mónada:
- Un constructor de tipo como “A” que dado un tipo de retorno como “int” devuelve un tipo “A<int>” que engloba tanto ese tipo de retorno como los efectos secundarios.
- Un par de funciones “bind” y “unit” que tienen los tipos antes mencionados.
- Que se cumplan las propiedades de elemento neutro y asociativa.
De los lugares en los que habitan las mónadas
La parquedad de los requisitos de las mónadas hace que aparezcan por todos los lados y no únicamente como modelo de efectos secundarios. Son en general un modelo de computación (ver ejemplo 1.1 en el articulo original de Moggi para una lista de cosas que puede modelar una mónada).
Por ejemplo, los punteros con NULL se usan generalmente como mónadas. El constructor de tipo está claro que es el de los punteros. De “int” pasamos a “int*”. La función “unit” es simplemente obtener la dirección de un entero.
int a;
int* p=&a; // p=unit(a)
La función “bind” consiste en comprobar que el puntero no es NULL.
return p==NULL ? NULL : p->OperaYDevuelvePuntero() ;
// return bind(p, OperaYDevuelvePuntero);
Es fácil comprobar las propiedades correspondientes con estas operaciones, pero aún hay más. Cualquier colección iterable es una mónada. Sí, así a lo bestia: vectores, conjuntos, listas, mapas, tablas hash, etc. Todos son mónadas. El constructor de tipo es el de la colección que queramos. Por ejemplo, “vector<int>”.
La función “unit” es bien sencilla: la colección con un único elemento.
vector<int> v;
v.push_back(3);
// v=unit(3)
La función “bind” es equivalente a iterar y mezclar.
vector<int> r;
foreach (x in v) r.append(Procesa(x));
// r=bind(v, Procesa)
Ojo que “Procesa” devuelve un vector y “append” mezcla vectores. Si “Procesa” fuera obtener la lista de divisores, entonces
bind([1, 6, 21], Procesa) = [1, 1, 2, 3, 6, 1, 3, 7, 21]
Esta propiedad del “bind” de separar, iterar y combinar es la que le da tanta utilidad. De hecho, debido a esto, “Procesa” también serviría para filtrar, transformar, unir y casi cualquier otra operación que se quiera realizar con la colección. Lo que no quita para que también la colección tenga sus operaciones propias no monádicas.
Pero con todo esto habría ya material para otra entrega en la que tendríamos que hablar de comprensiones monádicas, la notación “do” y empezar a usar muchas funciones anónimas.
domingo, 13 de marzo de 2011
miniSL parte 11 - Operaciones sobre el montículo
Ya hemos descrito el montículo en la parte octava. Ahora vamos a realizar dos tipos de operaciones sobre él. El primer grupo es el de las operaciones de reserva de memoria, mientras que el segundo grupo son las operaciones de liberado de memoria. En este post veremos las del primer grupo.
Inicialmente tenemos la creación de una celda genérica con dos referencias.
Somos astutos y antes de reservar memoria (con el push_back) vemos si tenemos alguna celda libre ya reservada. Esto es algo ineficiente porque la celda que reservemos no vuelve a liberarse realmente, sólo se apunta como liberada. Todo sea por ser simples en la implementación.
Para crear celdas de otros tipos, primero creamos una celda genérica con Script::CreateCell y luego cambiamos sus campos específicos. Por ejemplo, para una cadena no interna.
En el caso de una cadena interna hemos de recurrir a las técnicas comentadas en la parte séptima. En concreto, usaremos el mapa m_InternedStrings para comprobar si ya tenemos o no la cadena internada. Si es así, la usamos. Si no, la creamos y la guardamos en el m_InternedStrings.
Aquí se ve el truco comentado en la parte séptima: se usa la propia clave del mapa como la cadena interna. Esto nos fuerza a realizar la inserción en dos partes. Primero la celda de tipo NAME_CODE sin ningún puntero iniciado y, luego, se inicia el puntero string_val a la dirección de la clave i->first.
Para crear un entorno necesitamos crear adicionalmente su tabla de símbolos.
Y más sencillo aún son las funciones nativas porque son trozos de código que no se elimina nunca. En este caso necesitamos una función especial meramente porque el tipo es NATIVE y no CELL.
Con esto está la creación de celdas completada. En el siguiente apartado veremos cómo se usa el recolector de basura (garbage collector) del cual ya adelantamos algo en la parte octava.
Inicialmente tenemos la creación de una celda genérica con dos referencias.
CELL& Script::CreateCell(CELL_TYPE ct, CELL* first, CELL* second)
{
CELL* p;
if(m_FirstUnused==NULL)
{
CELL c;
m_Cells.push_back(c);
p=&m_Cells.back();
}
else
{
p=m_FirstUnused;
m_FirstUnused=p->next_unused;
}
p->mark=false;
p->type=ct;
p->head=first;
p->tail=second;
return *p;
}Somos astutos y antes de reservar memoria (con el push_back) vemos si tenemos alguna celda libre ya reservada. Esto es algo ineficiente porque la celda que reservemos no vuelve a liberarse realmente, sólo se apunta como liberada. Todo sea por ser simples en la implementación.
Para crear celdas de otros tipos, primero creamos una celda genérica con Script::CreateCell y luego cambiamos sus campos específicos. Por ejemplo, para una cadena no interna.
CELL& Script::CreateString(STRING const& val)
{
CELL& c=CreateCell(STRING_LIT);
c.string_val=new STRING(val);
return c;
}En el caso de una cadena interna hemos de recurrir a las técnicas comentadas en la parte séptima. En concreto, usaremos el mapa m_InternedStrings para comprobar si ya tenemos o no la cadena internada. Si es así, la usamos. Si no, la creamos y la guardamos en el m_InternedStrings.
CELL& Script::CreateName(STRING const& val)
{
STRING_MAP::const_iterator i=m_InternedStrings.find(val);
if(i==m_InternedStrings.end())
{
CELL& c=CreateCell(NAME_CODE);
i=m_InternedStrings.insert(std::make_pair(val, &c)).first;
c.string_val=&i->first;
}
return *i->second;
}Aquí se ve el truco comentado en la parte séptima: se usa la propia clave del mapa como la cadena interna. Esto nos fuerza a realizar la inserción en dos partes. Primero la celda de tipo NAME_CODE sin ningún puntero iniciado y, luego, se inicia el puntero string_val a la dirección de la clave i->first.
Para crear un entorno necesitamos crear adicionalmente su tabla de símbolos.
CELL& Script::CreateEnvir(CELL* parent)
{
CELL& c=CreateCell(ENVIR_VAL);
c.envir_table=new ENVIR_TABLE;
c.parent_envir=parent;
return c;
}Y más sencillo aún son las funciones nativas porque son trozos de código que no se elimina nunca. En este caso necesitamos una función especial meramente porque el tipo es NATIVE y no CELL.
CELL& Script::CreateNative(NATIVE native)
{
CELL& c=CreateCell(NATIVE_VAL);
c.native=native;
return c;
}Con esto está la creación de celdas completada. En el siguiente apartado veremos cómo se usa el recolector de basura (garbage collector) del cual ya adelantamos algo en la parte octava.
Etiquetas:
manejo de memoria,
miniSL
viernes, 4 de marzo de 2011
Estándar WebGL 1.0 publicado
Llevamos unos días con noticias sobre nuevos estándares que no paramos. Ayer, tres de marzo, salió otro estándar. Esta vez es WebGL, un contexto de renderización para el elemento CANVAS de HTML5. Cada vez los programadores de Javascript sobre la web tienen más y más recursos multimedia. ¿Será capaz el HTML5 de desbancar a otros sistemas como Flash o Silverlight como se proponía?
jueves, 3 de marzo de 2011
Tenemos finalistas para el SHA-3
Los SHA (secure hash algorithm) son una serie de algoritmos establecidos por la Agencia Americana de Tecnología para la criptografía. Si no sabes mucho de criptografía, puedes aprender todo lo que hace falta saber en una hora. Parece ser que según van saliendo los algoritmos se van buscando sus fallos y, por ejemplo, ya te avisan de que no uses el SHA-1 y que vayas pasándote al SHA-2. Es probable que de aquí a poco también empiecen a aparecer grietas en este último por lo que es importante ir preparándose para el SHA-3.
El SHA-3 no está decidido aún, pero el concurso ha llegado a su final donde sólo quedan cinco candidatos posibles. Los nombres de los algoritmos son:
Edit: El ganador fue Keccak. Así que ahora el SHA-3 es ese algoritmo.
El SHA-3 no está decidido aún, pero el concurso ha llegado a su final donde sólo quedan cinco candidatos posibles. Los nombres de los algoritmos son:
- BLAKE
- Grøstl
- JH
- Keccak
- Skein
Edit: El ganador fue Keccak. Así que ahora el SHA-3 es ese algoritmo.
miércoles, 2 de marzo de 2011
Unicode 6.0
Hace unos días se publicó la nueva versión del estándar Unicode. No hay cambios significativos, únicamente la introducción de nuevos caracteres. La lista diferencial de cambios está aquí y las tablas de códigos completas aquí.
Etiquetas:
varios
Suscribirse a:
Comentarios (Atom)