Supongamos que tenemos un evento que se dispara a una frecuencia dada [$f_0$] (por ejemplo, una frecuencia de muestreo). Llamaremos eventos básicos a estos eventos. Es fácil comprobar que puedo generar otros eventos derivados a partir de estos eventos básicos. Bastará tomar una frecuencia divisora [$f=f_0/k$] y lanzar un evento derivado cada [$k$] eventos básicos. Por ejemplo, si [$k=3$] tengo un evento derivado cada tres eventos básicos.
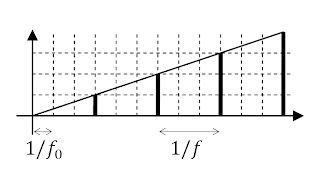
Si trazamos el número de evento básico en el eje de abscisas y el número de evento derivado en el eje de ordenadas, obtenemos una línea. En este caso, de pendiente [$1/3=f/f_0$].
¿Pero qué ocurriría si la frecuencia es una fracción cualquiera de [$f_0$] y no exactamente un divisor?
El algoritmo
En este caso a veces tendremos que contar [$k$] eventos básicos y otras veces [$k+1$]. No obtenemos una frecuencia exacta, pero en promedio sí será la [$f$] deseada. Pagamos un jitter por tener una frecuencia que no es divisora de la frecuencia básica.
Lo interesante aquí es que seguimos obteniendo una recta, aunque ya no está centrada en el origen y tampoco tiene una pendiente [$1/k$]. Si llamo [$0\le r<1$] a la altura de intersección con el eje de ordenadas y [$t$] al número de evento básico (en definitiva, es el tiempo transcurrido) mi recta es
[$$y=r+\frac{f}{f_0}t$$]
El primer evento derivado se tendrá que lanzar cuando la recta corte a la línea [$y=1$]. Es decir
[$$1=r+\frac{f}{f_0}t$$]
Debido a que el resultado puede no ser un número entero, hemos de redondear al siguiente evento básico que llamaremos [$t_1$].
[$$t_1=\left \lceil \frac{1-r}{f/f_0} \right \rceil$$]
Ya sabemos cuándo lanzar el siguiente evento derivado: será en el evento básico [$t_1$]. Lo interesante aquí es que puedo trasladar de nuevo todo al origen de coordenadas y calcular el valor [$r$] para el siguiente evento derivado empezando desde cero. Usando exactamente las mismas ecuaciones.
Este nuevo valor de [$r$], que llamaré [$r_1$], será el valor de [$r$] en [$t_1$] pero restando [$1$] para volver al origen de coordenadas.
[$$r_1=r+\frac{f}{f_0}t_1-1$$]
Con lo que el algoritmo sería
- Iniciamos con [$r=0$] y el valor [$f=f_0$] de frecuencia que deseemos.
- Calculamos [$t_1$] y [$r_1$] a partir del valor de [$r, f$] y [$f_0$].
- Esperamos [$t_1$] eventos básicos antes de lanzar un evento derivado.
- Hacemos [$r \leftarrow r_1$] y vamos al paso 2
La implementación
Este algoritmo está muy bien, pero hay un detalle de implementación. Tanto el valor [$f/f_0$] como el valor [$r$] están en el intervalo [$[0,1)$]. No es descabellado usar una notación de coma fija para representarlo en [$n$] bits. Entonces, usando el subíndice [$p$] para la coma fija,
[$$f_p=2^n \frac{f}{f_0} $$]
[$$r_p=2^n r$$]
Y las ecuaciones quedan
[$$t_1=\left \lceil \frac{2^n-r_p}{f_p} \right \rceil $$]
[$$r_1=r_p+f_p t_1-2^n$$]
La ecuación de [$t_1$] tiene un problema: el redondeo por exceso. Generalmente las divisiones enteras tienen redondeo por defecto. Es fácil hacer la conversión sumando el denominador menos uno.
[$$t_1=\left \lceil \frac{2^n-r_p}{f_p} \right \rceil=\left \lfloor \frac{2^n-r_p+f_p-1}{f_p} \right \rfloor $$]
Y un paso más es darnos cuenta que [$2^n-1-r_p$] no es más que el complemento a uno de [$r_p$] que notaremos [$ \sim r_p $].
[$$t_1=\left \lfloor \frac{\sim r_p+f_p}{f_p} \right \rfloor $$]
La ecuación de [$r_1$] puede simplificarse también ya que sumar o restar [$2^n$] no tiene efecto en aritmética módulo [$2^n$] por lo que llegamos a
[$$r_1=r_p+f_p t_1$$]
El algoritmo sigue siendo el mismo.


0 comentarios:
Publicar un comentario