El filtro de Butterworth
Aproximar la función [$F^2 (\omega)$] que debería valer 0 si [$\omega < \omega_p$] e infinito si [$\omega > \omega_s$] es muy sencillo. Todas las funciones monótonas (siempre crecientes) lo aproximan con más o menos éxito.
Una [$F^2 (\omega)$] muy usada es [$$F^2 (\omega)= \epsilon _p^2 \left(\frac{ \omega }{ \omega_p } \right)^{2n}$$] Este es el llamado filtro de Butterwoth. El número [$n$] es el orden del filtro. Debido a que debemos trabajar con polinomios, las potencias han de ser números naturales y, por tanto, el orden del filtro n debe ser un número natural. El orden del filtro está relacionado con el número de componentes eléctricos que va a tener nuestro circuito.
Construyamos su respuesta en frecuencia al cuadrado. [$$ |H(j\omega)|^2=\frac{1}{1+\epsilon_p^2 \left(\omega/\omega_p \right)^{2n}}$$] El filtrado de frecuencias que hace este filtro se muestra a continuación. Esta gráfica es la original del artículo de Butterworth de 1930 y representa [$|H(j\omega)|$] con [$\omega_p=1$].
 |
| Respuesta en frecuencia de un filtro de Butterworth tal cual aparecía en su artículo de 1930. |
El valor [$\epsilon_p$] está explícitamente escrito en la ecuación, pero no sabemos nada de [$\epsilon_s$]. Hemos de usar la expresión de [$|H(j\omega) |^2$] para deducir qué valor tendremos para [$\epsilon_s$]. Bastará calcular la respuesta en frecuencia a la frecuencia [$\omega_s$]. [$$|H(j\omega_s ) |^2=\frac{1}{1+\epsilon_p^2 \left(\omega_s/\omega_p\right)^{2n}} = \frac{\epsilon_s^2}{1+\epsilon_s^2}$$][$$ \frac{1}{\epsilon_s^2}=\epsilon_p^2 \left(\frac{\omega_s}{\omega_p}\right)^{2n},\ \ \ \ \epsilon_s \epsilon_p=\left( \frac{\omega_p}{\omega_s}\right) ^n$$] Esta última expresión, muy simple gracias a la introducción de los épsilon en la parte anterior, relaciona el orden del filtro con los requisitos. Como el orden del filtro ha de ser un natural, es usual escribir la ecuación como una cota. [$$ n \ge \frac{log(\epsilon_s \epsilon_p)}{log \left( \frac{\omega_p}{\omega_s} \right) } $$]
Polos y ceros
La función [$|H(j\omega) |^2$] está relacionada con la respuesta en frecuencia del filtro [$|H(j\omega) |$] sin cuadrado, pero lo que nos interesa para poder implementar el filtro es la función de transferencia [$H(s)$] que abarca todos los complejos. Los pasos son los siguientes.
Primero, con un cambio de variables [$\omega=-js$], convertimos [$|H(j\omega) |^2$] en [$|H(s) |^2$]. [$$ |H(s)|^2=\frac{1}{1+\epsilon_p^2 \left(-js/\omega_p \right)^{2n}}$$]
A continuación, obtendremos la función [$|H(s) |^2$] como un cociente de dos polinomios. Escribiremos los polinomios factorizando sus raíces. [$$|H(s) |^2=A^2 \frac{\prod{s-s_{cero m} }}{\prod{s-s_{polo m} }}$$] Las raíces del numerador se llaman ceros porque cuando [$s$] sea un [$s_{cero}$], tendremos que [$|H(s) |^2=0$]. Las raíces del denominador se llaman polos porque cuando [$s$] tienda a un [$s_{polo}$], todo [$|H(s) |^2$] tiende a infinito. El por qué se llaman polos es obvio cuando se hace la gráfica en tres dimensiones.
 |
| Visión 3D de la función de transferencia de un filtro de Butterworth. Se observan los polos y la respuesta en frecuencia cuya parte positiva está remarcada en rojo. |
Los filtros de Butterworth no tienen ceros. Esto ocurre porque el numerador de [$|H(s) |^2$] es uno. Pero sí tienen polos cuando el denominador se anula. Es decir, cuando [$F^2 (\omega)=-1$].[$$F^2 (-js_{polo} )=-1$$][$$\epsilon_p^2 \left(\frac{-js_{polo}}{\omega_p}\right)^{2n}=-1$$][$$\epsilon_p \left(\frac{-js_{polo}}{\omega_p}\right)^n=j$$][$$ \sqrt[n]{\epsilon_p}\frac{-js_{polo}}{\omega_p}=\sqrt[n]{j}$$][$$s_{polo}=\frac{j \omega_p}{\sqrt[n]{\epsilon_p}} \sqrt[n]{j}$$]
Usando las raíces de la unidad, llegamos a que los polos de [$|H(s) |^2$] yacen en un círculo. Como hay más de uno, los numeramos con un subíndice [$m$]. [$$s_{polo\ m}=\omega_p \epsilon_p^{\frac{-1}{n}} e^{j\left[\frac{p}{2}+\frac{p}{2n}+\frac{2p}{n} m\right]}$$] Es interesante localizar los polos en el plano de Argand (plano complejo). El siguiente diagrama muestra los polos de [$|H(s) |^2$] de un filtro de Butterworth de orden tres.
 |
| Distribución de los polos de la función de transferencia al cuadrado de un filtro de Butterworth de orden tres. |
Obteniendo la función de transferencia
La simetría que aparece en el diagrama anterior es usual en [$|H(s) |^2$] y se llama simetría cuadrantal. Ocurre que [$$|H(s) |^2=|H(-s) |^2=|H(s^* ) |^2$$] por lo que la función [$|H(s) |^2$] queda completamente definida por lo que pase en sólo uno de sus cuadrantes. Esta simetría se usa para obtener [$H(s)$] a partir de [$|H(s) |^2$] mediante la siguiente ecuación: [$$|H(s) |^2=H(s)H(-s)$$] Recordemos que [$|H(s) |^2$] estaba descrita como un producto de polos y ceros. Entonces, podemos separar los polos que van para [$H(s)$] y los que van para [$H(-s)$].[$$ A^2 \frac{\prod{(s-s_{cero\ m})}}{\prod{(s-s_{polo\ m})}}=\left[A \frac{\prod{(s-s_{cero\ de\ H(s)\ m})}}{\prod{(s-s_{polo\ de\ H(s)\ m} )}}\right]\left[A \frac{\prod{(s-s_{cero\ de\ H(-s)\ m} )} }{\prod{(s-s_{polo\ de\ H(-s)\ m}) } }\right]$$] Lo que sí que hay que decidir es qué polos van para [$H(s)$] y qué polos van para [$H(-s)$]. Es fácil. Para que [$H(s)$] sea realizable físicamente y estable, hay que escoger los polos cuya parte real sea negativa. Y para que el filtro sea de fase mínima (menor dispersión) también cogeremos los ceros que tengan su parte real negativa.
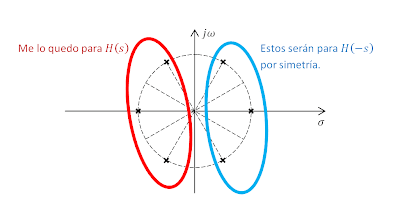 |
| Separación de los polos de [$|H(s)|^2$] que van para [$H(s)$] de los que van para [$H(-s)$]. |
Una vez tenemos [$H(s)$] podemos usar alguna de las técnicas de síntesis de circuitos para realizar el filtro.
Continúa en la parte tres.

0 comentarios:
Publicar un comentario