Lo que nunca me enseñaron: Los filtros de Cauer (parte III)

La primera parte está aquí y la segunda parte aquí.

Los viajes del arcocoseno

Hasta aquí todo lo visto ha sido para entender el proceso de realización de un filtro. A partir de aquí empezamos a acercarnos a los filtros elípticos. Sin embargo, antes debemos pararnos a explorar los filtros de Chebyshev. Los filtros de Chebyshev son más simples porque usan para su expresión matemática la circunferencia en vez de la elipse. Deberían llamarse filtros circulares, pero ya se ha quedado el nombre de Chebyshev.

Lo primero que necesitamos para entender los filtros de Chebyshev es la definición de arcocoseno. [$$arccos(x)=\int_x^1{\frac{dt}{\sqrt{1-t^2}}}$$] Esta integral no es más que la longitud de arco de una circunferencia unitaria desde una abscisa [$x$]. (Nota: Por supuesto, es una función multivaluada. Tomaremos sólo la rama de la raíz principal aquí).

El arcocoseno no es más que la longitud del arco marcado.

Lo sorprendente es que esta integral, el arcocoseno, tiene sentido cuando [$x$] va más allá de [$\pm 1$]. Eso sí, hemos de usar números complejos porque el radicando que aparece en la raíz se hace negativo.
Dibujaremos el valor que toma el arcocoseno en el plano de Argand conforme [$x$] tome valores reales. Empezaremos por el arcocoseno de cero que es [$\pi/2$].

El arcocoseno de cero es [$\pi/2$].

Si vamos aumentando [$x$], llegamos hasta [$arccos(1)=0$] obteniendo únicamente números reales. Es el arcocoseno clásico. Igualmente, si disminuimos [$x$], llegamos hasta [$arccos(-1)=\pi$]. Esta simetría continuará por lo que no hablaremos más de los valores negativos de [$x$].

El recorrido desde el arcocoseno de cero al arcocoseno de uno (y menos uno).

En el punto [$arccos(1)=0$] ocurre que la raíz del integrando se anula. [$$\sqrt{1-t^2 }=0$$] Si seguimos moviendo [$x$] por la recta real, el arcocoseno entrará en el eje imaginario. A partir de aquí tenemos otras dos ramas, la raíz positiva y la negativa. Elegimos la positiva y recordamos para luego que hay simetrías.

El recorrido del valor del arcoseno de los números reales.

Las olas del coseno

En los complejos, el coseno es una función holomorfa. Una de sus particularidades es la periodicidad en el eje real. Si trazamos su diagrama de ceros (no tiene polos) y añadimos algunos puntos destacados en la línea real obtenemos lo siguiente.

Los valores destacados que toma el coseno cuando su argumento es un número complejo.

Si recorremos el plano de Argand por la línea real [$x=\sigma$], obtenemos la función coseno clásica. El lado más oscuro corresponde a los valores negativos.

Los valores del coseno cuando su argumento es un número real ([$\omega=0$])

Si recorremos el coseno por la recta imaginaria obtenemos el coseno hiperbólico. Es importante darse cuenta que por estos dos recorridos el coseno siempre proporciona un valor real.

Los valores del coseno cuando su argumento es un número imaginario ([$\sigma=0$])

Como era de esperar, al ser el arcocoseno la función inversa del coseno, si hacemos el recorrido del arcocoseno desde 0 hasta infinito, vamos visitando los argumentos cuyo coseno se mueve desde 0 hasta infinito.

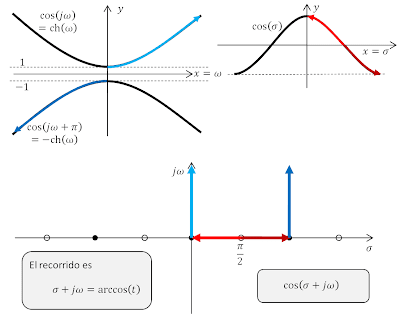Los valores del arcocoseno recorren los argumentos del coseno cuyo resultado es el argumento del arcocoseno. Son funciones inversas una de otra.

Los polinomios de Chebyshev

Los polinomios de Chebyshev se definen así: [$$C_n (x)=cos(n\ arccos(x) )$$] Para ver cómo son, observemos el recorrido de [$n\ arccos(x)$] sobre la función coseno. Es muy sencillo porque lo único que hacemos al multiplicar por [$n$] es ampliar fotográficamente [$n$] veces el recorrido del arcocoseno. En el siguiente diagrama usamos [$n=3$].

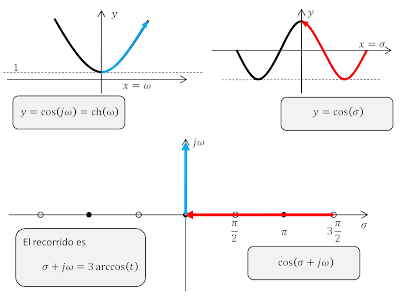El polinomio de Chebyshev de orden tres se obtiene ampliando por tres el recorrido del arcocoseno (la gráfica de abajo) y, luego, realizar el coseno (las dos gráficas de arriba).

Ampliar tres veces el recorrido no cambia mucho el valor del coseno por la recta imaginaria. Lo hace más abrupto porque nos movemos más rápidamente hacia el infinito. En donde sí que hay un cambio es en la parte real donde tenemos tres cuartos de pi en vez de uno. Esto hace que se oscile en esa parte.

Recordemos que en estas rectas todos los valores del coseno son reales y que hay otra parte simétrica cuando [$t\lt 0$]. Con esto en mente podemos dibujar [$C_3$].

Polinomio de Chebyshev de orden tres.

Observando con cuidado el recorrido de arriba, vemos que atraviesa exactamente 3 ceros del coseno: el [$\pi/2$] y su simétrico en [$5 \pi/2$] y el [$3 \pi/2$] que es su propio simétrico. Además, no es casual que los puntos donde [$x=\pm 1$] tome el valor [$y= \pm 1$] ya que son los puntos de arcocoseno nulo.

Una manera fácil de calcular los polinomios de Chebyshev es la siguiente. [$$C_{n+1} (x)=cos(n\ arccos(x)+arccos(x) )=x C_n (x)+sin(n\ arccos(x) ) sin(arccos (x) )$$][$$ C_{n-1}(x)=cos(n\ arccos(x)-arccos(x) )=x C_n (x)-sin(n\ arccos(x) ) sin(arccos(x) )$$] Sumando se llega a [$C_{n+1} (x)+C_{n-1} (x)=2 x C_n (x)$] y despejando [$C_{n+1} (x)$] se obtiene la siguiente fórmula recursiva. [$$C_{n+1} (x)=2 C_n (x) - C_{n-1} (x)$$] Usando la definición se obtiene que [$C_0 (x)=1$] y [$C_1 (x)=x$] con lo que tenemos todos los datos para calcular el polinomio de Chebyshev del orden que queramos.

El filtro de Chebyshev

La función [$C_n^2 (\omega)$] es una buena aproximación de [$F^2 (\omega)$]. Dibujemos su gráfica para n=3.

El polinomio de Chebyshev de tercer grado al cuadrado como aproximación a [$F^2(\omega)$].

Para que cumpla los requisitos de un filtro hay que ajustarla un poco. [$$ F^2 (\omega)=\epsilon_p^2 C_n^2 \left(\frac{\omega}{\omega_p} \right)$$]

La función [$F^2(\omega)$] de un filtro de Chebyshev.

Así que un filtro de Chebyshev es el que tiene la siguiente respuesta en frecuencia al cuadrado. [$$ |H(j\omega) |^2=\frac{1}{1+\epsilon_p^2 C_n^2 \left(\frac{\omega}{\omega_p} \right)}$$] A partir de aquí procedemos como en el filtro de Butterworth. Calculamos [$\epsilon_s$], despejamos [$n$] para el orden; calculamos los polos de [$|H(s) |^2$] (este filtro no tiene ceros) y separamos los polos para obtener [$H(s)$].

Todo esto lo dejaremos para el lector que observará, entre otras cosas, que el orden requerido es menor en un filtro de Chebyshev que en un filtro de Butterworth para los mismos requisitos.

El lector curioso queda emplazado para explorar los filtros inversos de Chebyshev e intentar usar la misma técnica de inversión para los filtros de Butterworth.

Continúa y acaba en la cuarta parte.