El algoritmo de la playa de agujas

Existe una gran variedad de posibles traducciones para el nombre de este algoritmo. El original en inglés es "shunting-yard algorithm". Esto de "shunting-yard" se podría traducir como patio de maniobras, playa de maniobras, playa de agujas o estación de clasificación. Como el nombre "shunting-yard" no es común, he elegido otro nombre poco común como "playa de agujas".
Las estaciones clasificadoras
Bueno, y a todo esto, ¿qué es una playa de agujas o una playa de maniobras? Es un tipo de estación de tren que sirve para desensamblar y ensamblar trenes. Su modo de funcionamiento es muy simple.
Tenemos dos haces de vías que convergen en una única vía. Las agujas son el mecanismo que permite conmutar entre dos vías convergentes. De ahí el nombre de este tipo de patio. La vía común, además, suele estar en lo alto de un montículo. La gravedad, como veremos, es importante. Un pequeño esquema de cómo funciona (con unas modestas dos vías por haz) está aquí abajo.

Primero se sube el tren que queremos desensamblar a la colina. Entonces se seleccionan las vías por las que queremos que caigan los vagones. Finalmente, se sueltan los vagones y se quitan los frenos. La gravedad hace el resto.

Todo esto está muy bien, pero ¿qué tiene que ver con la algoritmia?
Las prioridades de los operadores
Cuando escribimos una expresión como 1+3*5 el significado es realmente 1+(3*5). Esto es así porque decimos que la multiplicación tiene más precedencia (o más prioridad) que la suma y por eso se hace antes. Un humano rápidamente va detectando y evaluando primero los operadores con mayor precedencia, pero cuando le introducimos a un algoritmo una cadena como 1+3*5 la cosa no es tan sencilla.
Uno de los padres de la informática, E.W.Dijkstra, ideó el algoritmo que permite calcular estas expresiones teniendo en cuenta las prioridades de los operadores involucrados. El algoritmo terminó siendo llamado "shunting-yard algorithm" porque funcionaba como una playa de agujas.
La idea principal del algoritmo es muy simple. Vamos clasificando la entrada en operadores y operandos, cual si fueran vagones de primera o de segunda. Cuando tenemos dos operadores, comparamos las prioridades y vamos ensamblando los vagones de mayor prioridad (es decir, calculamos las operaciones).

Por partes, como decía mi profesor de matemáticas.
Calculando 1+3*5
Introduzcamos 1+3*5 en el algoritmo. Pondremos los vagones con la entrada abajo a la derecha.
El algoritmo empieza clasificando los operadores y los operandos. Los primeros irán arriba a la izquierda y los segundos abajo a la izquierda.


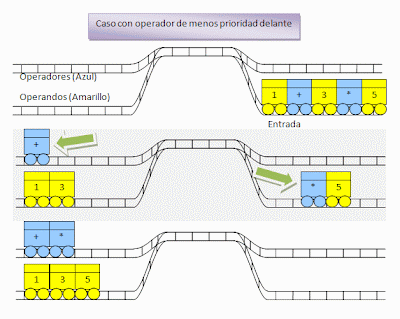
El punto clave ocurre cuando tenemos que introducir el vagón con * junto al vagón con +. Como * tiene más prioridad que el +, no ocurre nada y la clasificación termina normalmente.

En este punto realizamos todas las operaciones. Esto suele forzarse introduciendo un "vagón fantasma" con la menor prioridad posible pero en esta explicación, y para no liarnos, sencillamente completamos los cálculos cuando no haya más entrada.

Las operaciones se realizan ensamblando dos operandos (los vagones amarillos) con el último operador (el vagón azul más a la derecha de los operadores). El resultado 15 es un operando para el siguiente operador, la suma +.

La suma se realiza de la misma manera sacando dos operandos amarillos y ensamblando los vagones con el operador + en medio. El resultado es otro vagón amarillo que, en nuestro caso, ya tiene el resultado final: 16.
Calculando 2*4+6
Ahora vamos a poner el operador de más prioridad delante. Todo empieza igual, clasificando los vagones en operadores azules y operandos amarillos.  Sin embargo, cada vez que intentemos introducir un operador en la vía de arriba a la izquierda, hemos de comprobar las prioridades.
En este caso, el + tiene menos prioridad que el * lo que significa que antes de introducir el + hemos de calcular la multiplicación.


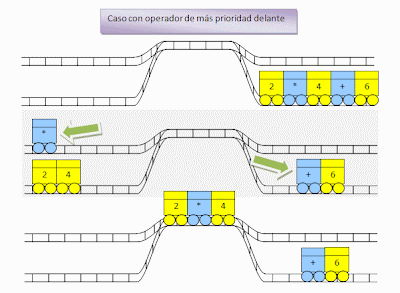
Como siempre que realizamos una operación, el resultado se guarda en un vagón amarillo que será un operador para la siguiente operación. ¡Pero espera! No hay operadores azules en la vía de arriba a la izquierda, hemos de seguir clasificando la entrada. Esto significa pasar el + y el 6 a la izquierda.

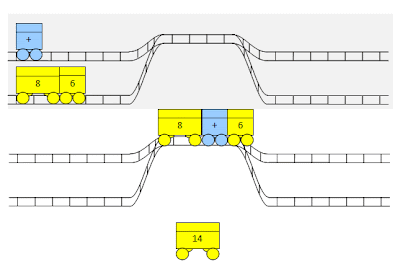
Finalmente, se nos acaba el tren de la derecha, la entrada, y hay que completar los cálculos. El resultado es el que esperábamos en un principio. ¡El algoritmo funciona!

Este algoritmo es relativamente importante cuando estamos trabajando con un reconocedor (parser) de un lenguaje de programación. En este caso en vez de calcular la operación, vamos construyendo el AST de la expresión. Esto es equivalente a obtener las versiones con paréntesis de las expresiones anteriores: 1+(3*5)   o   (2*4)+6.

Edit: He realizado una implementación recursiva del algoritmo en esta entrada.