domingo, 26 de diciembre de 2010
Por qué no existe el compresor perfecto o los nidos de las palomas
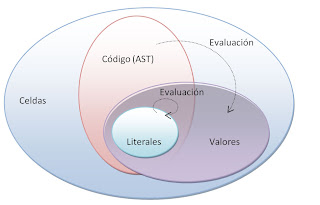
Está claro que
[$$c(0)=\epsilon$$]
Puesto que la cadena vacía [$\epsilon$] es la única cadena con menos longitud que la cadena [$0$]. ¡Pero también es inmediato para la cadena [$1$]!
[$$c(1)=\epsilon$$]
Entonces, ¿cuánto es [$ d(\epsilon) $]? Porque sólo podrá ser una de las dos cadenas iniciales, pero no las dos.
Esto es el llamado principio del palomar. Sólo tenemos una cadena de longitud cero para almacenar dos cadenas de longitud uno. Si en un palomar hay más pichones que nidos, en algún nido habrá dos pichones (y no podremos descomprimirlos).
Por tanto, no existe el compresor perfecto. Habrá cadenas que comprima y otras que expanda. El truco está en que comprima las cadenas más usadas y expanda las menos usadas.
lunes, 20 de diciembre de 2010
miniSL parte 7 - Las cadenas internas
Comparar cadenas es un algoritmo de complejidad O(n) lo que significa que va a ralentizar todo el proceso. Para solucionar esto la estrategia más común es usar lo que se llaman cadenas internas (interned string). De cada cadena interna sólo va a haber una única copia de forma que podamos usar su dirección para comparar cadenas. Así que la comparación de cadenas se reduce a una comparación de punteros.
Para convertir una cadena a su cadena interna bastará buscar la copia única o, si no existe aún, crearla.
STRING_MAP es el diccionario que a cada cadena le asigna una única copia. Esta copia será una celda del tipo NAME_CODE. De hecho, la única diferencia entre NAME_CODE y STRING_VAL es que en el primer caso la cadena es interna y en el segundo no (puede haber copias).
ENVIR_TABLE es ahora la tabla de símbolos que relaciona un NAME_CODE (el nombre de la variable) con un valor. Cada entorno tendrá un ENVIR_TABLE y un puntero opcional al entorno padre.
La clase Script, que contendrá todo el estado del intérprete del lenguaje que estamos creando, también tendrá que guardar el diccionario de cadenas internas. Lo haremos con la siguiente declaración de variable miembro privada.
STRING_MAP m_InternedStrings;
Los casos de uso serán buscar o crear una cadena interna y borrarla. El valor de la cadena es accesible mediante CELL::string_val.
La creación es algo más compleja que la destrucción ya que hemos de comprobar si ya está la cadena en nuestro diccionario.
CELL& Script::CreateName(STRING const& val)
{
STRING_MAP::const_iterator i=m_InternedStrings.find(val);
if(i==m_InternedStrings.end())
{
CELL& c=CreateCell(NAME_CODE);
i=m_InternedStrings.insert(std::make_pair(val, &c)).first;
c.string_val=&i->first;
}
return *i->second;
}
Aprovechamos que la implementación de std::map es un árbol (y no mueve los nodos por memoria una vez creados) para usar la propia cadena que hace de clave como la única copia de la cadena. Por esa razón hacemos c.string_val=&i->first. Esto no podría hacerse si la implementación fuera una tabla hash ya que estas tablas cambian de tamaño y requieren cambiar de posición de memoria las claves.
La destrucción, por otro lado, es sencilla.
m_InternedStrings.erase(*i->string_val);
Aunque hay que ver esta línea en el contexto del recolector de basura. Dedicaremos la siguiente entrada a implementar el recolector de basura.
miércoles, 8 de diciembre de 2010
C++: Conceptos y traits
Conceptos mediante traits
Antes de nada hay que entender que los template en C++ no pueden compilarse inmediatamente porque no sabemos los tipos que vamos a tener cuando instanciemos el template.
El problema podría ser resuelto si forzamos a que estos tipos cumplan un contrato, una interfaz. La idea es hacerlo mediante los llamados conceptos. Por ejemplo, un tipo sobre el que podamos comprobar la igualdad, tendría un concepto parecido a este:
concept Eq<T>
{
bool operator==(T const& l, T const& r);
}
Ahora podríamos agregar tipos que cumplen ese concepto mediante lo que se denomina una asignación de concepto (concept_map).
concept_map Eq<int>
{
bool operator==(int const& l, int const& r) { return l==r; }
}
Hay que notar que el == de los enteros no es inmediatamente Eq ya que el concepto Eq podría significar algo más que "tiene igual". Podría significar "tiene igual y es reflexivo, simétrico y transitivo" por lo que sólo el programador sabe si puede o no hacer un concept_map en función de la semántica del concepto.
La idea es que ahora, en un template, se pueda usar el igual del concepto en vez del igual de la clausura dinámica.
template<Eq T>
T f(T const& a, T const& b)
{
return a==b ? a : b;
}El == este sería el del concepto Eq y no una función que haya que esperar a tener el tipo T para encontrarla en tiempo de instanciación. Por tanto, este template se podría comprobar estáticamente en declaración. Sin saber si T es un int u otra cosa.
La manera de implementar algo parecido en el C++ actual (aunque sin la ventaja de la comprobación en declaración) es mediante el uso de traits. En vez de tener Eq como un concepto (ya que el C++ actual carece de ellos) lo tendremos como una clase Eq<T> que significa "el tipo T es del concepto Eq". Para que el tipo T sea del concepto Eq deberá demostrarse que el operador == es parte de ese tipo.
template<typename T>
class Eq
{
public:
static bool operator==(T const& l, T const& r);
};
El concept_map no es más que una especialización demostrando que int se ajusta a lo requerido. El compilador de C++ actual no lo comprueba así que hemos de ser cuidadosos.
template<>
class Eq<int>
{
public:
static bool operator==(int const& l, int const& r) { return l==r; }
};
Finalemente, cuando usemos estos sucedáneos de conceptos, hay que usar la clase trait en vez de utilizar directamente el operador ==. En el caso de los conceptos puros el uso del == del concepto era implícito.
template<typename T>
void f(T a, T b)
{
return Eq<T>::operator ==(a, b) ? a : b;
}
Lo importante aquí es que es posible mediante esta técnica el separar la comprobación del template de su instanciación. Desafortunadamente, este conocimiento ha llegado a la comunidad de C++ unos veinte años después de que se estandarizaran los templates (como ya he comentado en una entrada anterior, incorrectamente). Aunque usemos Eq<T>::operator ==(a, b), el compilador tomará esta expresión como dependiente y no la comprobará estáticamente.
Extensión hipotética de C++
Esto no quiere decir que no se puedan introducir. Sólo quiere decir que hay que tener muchísimo más cuidado en cómo se hace puesto que interacciona con otras características del C++ de maneras indeseadas lo cual llevó a retirar los conceptos del estándar actual.
Una manera posible de introducirlo, pienso, sería subsanando las dos carencias que hemos comentado arriba.
- Comprobar que las especializaciones implementan el template general.
- Evitar que se tomen como expresiones dependientes las que usen estos templates comprobados.
Postulemos entonces una pequeña variación en C++ introduciendo unos templates cuyas especializaciones tengan que implementar su interfaz forzosamente. Usaremos la hipotética sintaxis abstract template.
abstract template<typename T>
class Eq
{
public:
static bool operator==(T const& l, T const& r);
};Con esta hipotética sintaxis el compilador se quejaría de especializaciones como estas:
//ERROR: Eq<T> es abstract y su especialización Eq<int> no implementa ==
template<> class Eq<int>
{
public:
static bool operator<(int const& l, int const& r) { return l<r; }
};
//ERROR: El segundo argumento de operator == no es de tipo adecuado.
template<> class Eq<int>
{
public:
static bool operator==(int const& l, float const& r) { return l<r; }
};
Como el compilador sólo va a permitir las especializaciones que cumplan con el abstract template, tiene suficiente información para comprobar las expresiones que usen este abstract template, hayan sido especializadas o no. Por esta razón no es necesario que el uso de los abstract template sean dependientes.
template<typename T>
void f(T a, T b)
{
return Eq<T>::operator ==(a, b) ? a : b;
}
La expresión Eq<T>::operator ==(a, b), aunque depende de T, como lo hace a través de un abstract template, no es dependiente y se puede comprobar ahora. De hecho, se comprueba que operator== es miembro de Eq
Estas modificaciones que propongo son en principio seguras ya que si no introduces ningún abstract template todo sigue siendo compatible. No rompe ningún código. Son fáciles de realizar puesto que es añadir una pequeña regla en la definición de expresión dependiente y la comprobación de que se implementa una interfaz es bastante parecida a la de las funciones virtuales puras (aunque hay detalles y en los detalles está el diablo).
Otra cosa es que no cumpla todos los objetivos que se esperaban de los conceptos como su uso implícito. Vayamos por partes. Esto es un primer paso, veremos como solucionar el siguiente en otro momento.
Nota: Podríamos recurrir a la vinculación dinámica en vez de a un trait y tener
template<typename T>
class Eq
{
public:
bool (*operator==)(T const& l, T const& r); //Sin static
};Que se usaría así
template<typename T>
void f(Eq<T>& demo, T a, T b)
{
return demo.operator ==(a, b) ? a : b;
}
Ahora bien, ¿para qué retardar la decisión a tiempo de ejecución? Muy sencillo. Este cambio permite compilar el template y generar código. Esto es lo que se llama compilación separada y aceleraría los tiempos de compilación. Como siempre, hay un compromiso entre perder algo de tiempo de ejecución o perder algo de tiempo de compilación.
miércoles, 1 de diciembre de 2010
Expresiones dependientes en templates de C++
Existe un aspecto poco conocido a la hora de usar los templates de C++ que son las expresiones dependientes. Éstas dan un susto de vez en cuando a quienes las usan ya que son una mala implementación de las clausuras estáticas. El código ofensivo es el siguiente.
void f() { std::cout<<"A"; }
template<typename T>
struct B {
void f() { std::cout<<"B"; }
};
template<typename T>
struct D : public B<T> {
void g()
{
f(); //¿Imprime "A" o "B"?
}
};
int main()
{
D<char>::g();
}
Si llamamos a D<t>::g(), ¿se imprime "A" o se imprime "B"? Si se imprimiera "A" significa que se está usando el entorno global y si se imprime "B" significa que se está usando el entorno de la estructura D (que hereda de B). Esto está relacionado con la pregunta, ¿cuándo se compila/comprueba D? D se compila/comprueba parte cuando se declara (en el código de arriba donde pone template<typename T> struct D hasta la llave de cierre }; ) y parte cuando se instancia (cuando se hace T=char en D<char>::g() ).
Las clausuras
Teniendo en cuenta que main() está en el entorno global y la estructura D es el entorno local de la definición de g(), el problema aquí es distinguir entre la clausura dinámica o la clausura estática. La clausura dinámica significa que si no encontramos la definición de un nombre en una declaración, buscamos en el contexto donde se está usando esa declaración (en D<char>::g()) . La clausura estática busca en el contexto donde se está declarando la declaración (en template...).
En los lenguajes basados en entorno, como el LISP o el Scheme, se usa la clausura estática, también llamada clausura léxica. Esto impide comprobar con facilidad si nuestra declaración es correcta porque no tenemos aún los tipos a los que vamos a instanciar (el char). Claro que esto no es problema ni en LISP ni en Scheme porque son lenguajes dinámicos.
La decisión
La "solución" de los creadores de C++ fue separar la declaración del template en dos partes: la parte dependiente de los parámetros de tipos (los T) y la parte independiente de los mismos. La parte independiente puede comprobarse estáticamente, mientras que la parte dependiente se deja para cuando se conozca el argumento de tipo para la instanciación (el char).
El gran problema es que comprobar significa también buscar las declaraciones de los nombres y, en el caso de arriba, según f() sea del contexto estático o dinámico será la que imprime "A" o imprime "B".
Es fácil ver que la herencia de la clase D es B<T> y, efectivamente, depende de T por lo que no se va a buscar ningún nombre hasta el momento de instanciación ( D<char>::g() ). Antes de la instanciación está la declaración ( desde template<typename T> struct D hasta la llave de cierre }; ) y resulta que el f() que hay dentro de la declaración de g() no depende de T. Eso significa que se busca el nombre ahí, en declaración y el que encuentra es el que imprime "A" ya que el que imprime "B" depende de T a través de la herencia y no lo va a ver hasta la instanciación.
El resultado, contraintuitivo, es que imprime "A". Si tu compilador imprime "B", no se ajusta al estándar. Puedes ver más de esto en el FAQ del C++.
La historia se repite
Todo el lío fue la decisión, desde mi punto de vista errónea, de intentar comprobar el template en declaración, antes de tener los argumentos de tipos para instanciar. En el 90% de los casos al final no puedes comprobarlo en declaración porque casi todo va a depender de T, ¡que para algo se ha puesto! Así que la ganancia de separar las expresiones en dependientes e independientes es mínima y la pena es que se ha introducido la clausura dinámica por la puerta de atrás. La clausura dinámica es recordada amargamente por los programadores de LISP ya que hizo perder veinte años de investigación probando cosas como las FEXPR que al final tuvieron que ser descartadas.
In modern terminology, lexical scoping was wanted, and dynamic scoping was obtained (John McCarthy, History of Lisp)
Si se hubiera usado la clausura léxica, estos problemas no habrían surgido ya que se habría seguido la idea de sustitución (de hecho, esa fue la razón por la que se inventó la clausura léxica) y los costes habrían sido prácticamente los mismos que los que pagamos ahora.
El problema es que ahora estamos atados. De eso hablaré en otra entrada.
miércoles, 24 de noviembre de 2010
Por qué no sumar FPS y la ley de Amdahl
 |
| Pantalla del Crysis con grandes cantidades de vegetación que ralentizan el renderizado bajando los FPS a lo mínimo imprescindible para que la vista sea suave: 26, la cifra en la esquina superior derecha. El estándar de cine es de 24 FPS, pero las imágenes suelen contener movimiento. Generalmente esto es muy costoso de conseguir en tiempo real por lo que en los videojuegos el resultado es más brusco a esa misma tasa de fotogramas. |
Al trabajar con frecuencias contamos cuántas veces podemos realizar una operación que dura [$ t $] segundos. La frecuencia será precisamente
[$$ f=\frac{1}{t} $$]
Si añado algo a esa operación, me durará lo que duraba antes más el añadido [$ t+a $]. La nueva frecuencia será
[$$ f_a=\frac{1}{t+a} $$]
Generalmente no añadimos o quitamos nada. Simplemente, al cambiar una parte de nuestra operación, ésta se hace más larga o más corta. Es lo que pasaba con el desarrollador de videojuegos que cambiaba la manera de hacer algo y cambiaba su frecuencia de desempeño.
Supongamos que de todo ese tiempo [$ t $] solamente la fracción [$ p $] es la parte que tocamos. Esto quiere decir que la parte tarda en ejecutarse [$ tp $] y todo lo que no es la parte cambiada es [$ t(1-p) $].
El cambio que hago será probablemente una mejora. Si antes de la mejora tardaba [$ tp $] en realizar la operación de la parte a cambiar, después de una mejora de [$s$] veces tardará [$s$] veces menos. Es decir,
[$$ \frac{tp}{s} $$]
Como bien se sabe, en computación mejorar es ir más rápido haciendo algo. Tardamos menos tiempo así que dividimos. Ir el doble de rápido significa tardar la mitad.
Ahora voy a sumar los tiempos que tardo en la parte no mejorada y la parte mejorada. Es esta expresión:
[$$ \frac{tp}{s}+t(1-p) = t\left( \frac{p}{s} + (1-p) \right)$$]
Finalmente voy a obtener en vez del tiempo que tardo en hacer la operación completa, cuántas veces voy a poder realizarla. Esto es la frecuencia con mejora [$ f_s $].
[$$ f_s = \frac{1}{ t\left( \frac{p}{s} + (1-p) \right) } $$]
Afortunadamente podemos expresar esta frecuencia con mejora en función de la frecuencia sin mejora.
[$$ f_s = f \frac{1}{ \frac{p}{s} + (1-p) } $$]
El factor de mejora no es una suma como decía el desarrollador de videojuegos al hablar de FPS. El factor de mejora es una constante multiplicativa. Precisamente es
[$$ A = \frac{1}{ \frac{p}{s} + (1-p) } $$]
Esta expresión es la conocida Ley de Amdahl y el factor que calcula puede escribirse como un tanto por ciento. Habría sido más correcto entonces que el desarrollador de videojuegos hubiese dicho que perdía el 30% de rendimiento con el nuevo método.
miércoles, 17 de noviembre de 2010
miniSL parte 6 - Campos de celda
Además, necesitaremos según el tipo:
- UNUSED: Un puntero a la siguiente celda sin usar. De esta manera mantenemos una lista simplemente enlazada de las celdas sin usar.
- EMPTY_LIT: La lista vacía no requiere ningún valor adicional.
- INT_LIT: Un literal entero requiere el valor entero que almacena.
- STRING_LIT: Un literal de cadena requiere la cadena que almacena.
- LAMBDA_VAL: Un valor de función definida por el usuario requiere tres cosas: el código a ejecutar, los parámetros que tiene la función y la clausura léxica del código. Usaremos una lista para agrupar el código con los parámetros por lo que sólo requeriremos dos valores.
- NATIVE_VAL: Un puntero a la función nativa.
- ENVIR_VAL: Un puntero a la tabla hash o árbol de búsqueda que relaciona los nombres de las variables con sus valores. Además, otro puntero a el entorno padre (si existe) donde se buscarán los nombres que no se encuentren en la tabla de éste.
- BOOL_VAL: El valor verdadero o falso del booleano.
- NAME_CODE: Un puntero a la cadena con el nombre de la variable.
- COMBINE_CODE: El operador y sus operandos en una lista.
- CONS_CTOR: La cabeza y el resto de la lista.
Con todas estos campos en la cabeza, la estructura de una celda queda así:
struct CELL
{
CELL_TYPE type;
bool mark; //Garbage collection mark
union
{
CELL* next_unused; //UNUSED
int int_val; //INT_LIT
bool bool_val; //BOOL_VAL
STRING const* string_val; //STRING_LIT
CELL* head; //CONS.
CELL* code; //LAMBDA_VAL. The cell must be a CONS_CTOR with parameters and body
NATIVE native; //NATIVE_VAL
ENVIR_TABLE* envir_table; //ENVIR_VAL
CELL* op; //COMBINE_CODE. The cell must be code (Any *_CODE type or CONS or EMPTY)
};
union
{
CELL* tail; //CONS. Must be CONS or EMPTY.
CELL* closure; //LAMBDA_VAL. The cell must be an environment (ENVIR_VAL)
CELL* parent_envir; //ENVIR_VAL. The pointer may be NULL or an environment cell (ENVIR_VAL)
CELL* operands; //COMBINE_CODE. The cell must be a list of code.
};
};
La mayoría de los tipos de C++ que hemos usado han quedado por definir. En principio dependerán de la plataforma.
typedef std::wstring STRING; typedef std::wistream ISTREAM; typedef std::wostream OSTREAM; typedef std::map<STRING, CELL*> STRING_MAP; typedef std::map<CELL*, CELL*> ENVIR_TABLE; typedef std::deque<CELL> CELL_STORAGE; typedef CELL& (*NATIVE) (Script& script, CELL& args, CELL& envir);
En la siguiente entrada hablaremos con más tranquilidad de STRING_MAP y ENVIR_TABLE; en otra posterior hablaremos de CELL_STORAGE y, mucho después, de NATIVE, ISTREAM y OSTREAM.
miércoles, 10 de noviembre de 2010
Asincronía en C# 5.0
¿Qué tienen en común las siguientes características de C#? (Todas convenientemente explicadas por Eric)
Muy sencillo. Todas estas características se obtienen mediante una transformación sintáctica del código. Es decir. No hay una nueva semántica, sólo transformaciones sintácticas. ¿Y por qué es esto relevante? Porque se habrían evitado todo el follón si hubieran introducido un mecanismo de macros en el lenguaje. No algo tan crudo como el preprocesador de C. Quizás algo como los patrones de C++. O, mucho mejor, algo como las macros del LISP o Scheme.
Si es que al final volvemos al principio.
jueves, 4 de noviembre de 2010
miniSL parte 5 - Tipos de celda
Ahora que conocemos la sintaxis, sabemos qué tipos de celdas necesitamos para almacenar el código. De hecho, cada tipo de nodo del AST tendrá que ser una celda así que tenemos los siguientes tipos de celdas por ahora:
enum CELL_TYPE
{
UNUSED,
//Literals
EMPTY_LIT, INT_LIT, STRING_LIT,
//Value constructors
//Code constructors
NAME_CODE, COMBINE_CODE,
//Value and code constructors
CONS_CTOR
};
Finalmente debemos saber cuáles van a ser los resultados de nuestras evaluaciones. Aparte de los literales, usaremos tres valores.
- Los booleanos.
- Las funciones definidas por el usuario (lambda).
- Las funciones predefinidas (nativas).
enum CELL_TYPE
{
UNUSED,
//Literals
EMPTY_LIT, INT_LIT, STRING_LIT,
//Value constructors
LAMBDA_VAL, NATIVE_VAL, ENVIR_VAL, BOOL_VAL,
//Code constructors
NAME_CODE, COMBINE_CODE,
//Value and code constructors
CONS_CTOR
};
Ahora nos queda por saber qué información requiere cada tipo de celda y cómo vamos a almacenarla.
sábado, 30 de octubre de 2010
miniSL parte 4 - Sintaxis
Todo lenguaje de programación se puede reducir a una serie de combinaciones de operadores con sus operandos. En LISP esa combinación la produce la lista.
( operador operando1 operando2 … operandoN )
Si queremos introducir expresiones infijas y prefijas, necesitamos separar la lista por comas. En caso de no hacerlo, tendríamos la siguiente ambigüedad:
( operador 1 + 2 )
( operador 1 [+2] )
( operador [1+2] )
Una vez separada por comas, no hay dificultades en resolver la ambigüedad anterior.
( operador, 1, +2 )
( operador, 1+2 )
Es habitual usar la combinación preponiendo el operador y esa será nuestra sintaxis básica.
operador(1, +2)
Esta sintaxis es similar a las expresiones M del LISP y, al usarla, perdemos algo de la homoiconicidad. Es decir, la representación en memoria se aleja de la representación textual del código.
Mezclando operadores infijos, prefijos y postfijos obtenemos esta gramática informal.
exp -> infija
infija -> prefija | infija SIMBOLO infija
prefija -> postfija | SIMBOLO prefija
postfija -> primaria | postfija "(" lista_operandos? ")"
primaria -> ENTERO | CADENA | NOMBRE | "(" exp ")"
lista_operandos -> exp | exp "," lista_operandos
Los SIMBOLOs son cadenas de
!%&*+-/<=>?^|~
Más adelante estableceremos algunas restricciones sobre los símbolos. Los nombres cadenas de letras, dígitos y subrayado que no empiecen por dígitos. Las cadenas se expresarán entre comillas.
"Escribiremos las cadenas así"
Nada de esto está especificado en la gramática de arriba donde hemos usado los token SIMBOLO, ENTERO, CADENA y NOMBRE en los casos descritos. Por ahora no profundizaré en este aspecto ya que nos interesa saber cómo va a ser el AST, no cómo va a ser el análisis léxico (escaneado).
Todas las operaciones generan una combinación. Eso quiere decir que 1+2 se transforma en +(1,2) y que -7 se transforma en -(7). De esta manera, se consigue uniformidad en la representación pero legibilidad en el código. El resultado es que, tras estas transformaciones, toda la sintaxis se puede describir con cuatro tipos de nodos.
- Valores literales como 1 u "hola".
- Nombres como f o x.
- Combinaciones como f(x, x).
- Listas para almacenar la lista de operadores de una combinación. Aprovecharemos también para representar listas así [1, "hola", x].
- Nodo de nombre f.
- Node de nombre +.
- Nodo de literal entero 1.
- Nodo de literal entero 2.
- Nodo de lista vacía. Esto es la lista [].
- Nodo de construcción de lista a partir de los nodos 4 y 5. Esto es la lista [2].
- Nodo de construcción de lista a partir de los nodos 3 y 6. Esto es la lista [1,2].
- Nodo de combinación a partir de los nodos 2 y 7. Esto es la combinación +(1,2).
- Nodo de combinación a partir de los nodos 1 y 8. Esto es la combinación f(+(1,2)).
jueves, 28 de octubre de 2010
Semántica operacional de continuaciones
Sintaxis
Su sintaxis es la siguiente:
[$$ t::= x \mid \lambda x.t \mid tt \mid callcc \mid \#e $$]
Esto quiere decir que un término será o bien una variable, o bien una abstracción lambda, o bien una aplicación de un término sobre otro, o bien una llamada a call/cc o bien una continuación (con el [$ \# $] delante).
Como se observa, las continuaciones hacen uso de una nueva categoría sintáctica [$ e $]. Esta es la categoría de los términos con hueco. Debido a que vamos a evaluar primero el operador y luego el operando, en la última aplicación de esta categoría requerimos un valor a la izquierda.
[$$ e::= [] \mid et \mid ve $$]
Los valores son los ya conocidos más una continuación.
[$$ v::= \lambda x.t \mid x v_1 ... v_n \mid \#e $$]
Así que, en el fondo, una continuación no es más que una expresión con un hueco. Ese hueco hay que rellenarlo cuando utilicemos la continuación. Para eso hemos de definir primero la semántica.
Semántica
Esta semántica hace uso de los propios términos con hueco. Cuando escribimos [$ e[t] $] lo que queremos decir es un término con hueco [$ e $] rellenado el hueco con el término [$ t $]. En este caso, la regla β queda así:
[$$ e[(\lambda x.t)v] \rightarrow e[ [x \mapsto v] t] $$]
Que no es más que decir: allá donde haya una aplicación de una abstracción sobre un valor, sustitúyela por el término de la aplicación cambiando la variable ligada por el valor. Esta regla es usual en el lambda cálculo, aunque dentro de un término con hueco hecho explícito, así que no comentaré nada más.
El meollo del asunto está en modificar ese término con hueco y para eso usamos call/cc y la continuación.
[$$ e[callcc\ t] \rightarrow e[t (\#e)] $$]
[$$ e[(\#e') v] \rightarrow e'[v] $$]
Lo que hace call/cc es recordar el término con hueco, guardándolo en la continuación. Lo que hace la continuación es volver a ese término con hueco.
Ejemplo
De esta manera, usando las continuaciones, se pueden implementar las sentencias de control que queramos. Por ejemplo, un bucle, si suponemos que tenemos secuencia, variables y condicionales.
[$$ n=0;\ k=callcc\ (\lambda x. x)\ ;\ if\ n<5\ \{\ print\ n\ ;\ n=n+1\ ;\ k\ 0\ \} $$]
Evalúo [$ n=0 $]. Ahora [$ n $] vale [$ 0 $].
[$$ k=callcc\ (\lambda x. x)\ ;\ if\ n<5\ \{\ print\ n\ ;\ n=n+1\ ;\ k\ 0\ \} $$]
Evalúo [$ callcc $]. Es un paso importante porque todo lo que hay alrededor del call/cc pasa a ser la continuación.
[$$ k\ =\ (\lambda x. x)\ (\#\ []\ ;\ if\ n<5\ \{\ print\ n\ ;\ n=n+1\ ;\ k\ 0\ \} )\ ;\ if\ n<5\ \{\ print\ n\ ;\ n=n+1\ ;\ k\ 0\ \} $$]
Evalúo la aplicación de la abstracción lambda con la continuación. Es muy fácil porque es la función identidad por lo que el resultado es la propia continuación.
[$$ k\ =\ (\#\ []\ ;\ if\ n<5\ \{\ print\ n\ ;\ n=n+1\ ;\ k\ 0\ \}\ )\ ;\ if\ n<5\ \{\ print\ n\ ;\ n=n+1\ ;\ k\ 0\ \} $$]
Ahora [$ k $] vale la continuación [$ \#\ []\ ;\ if\ n<5\ \{\ print\ n\ ;\ n=n+1\ ;\ k\ 0\ \} $].
[$$ if\ n<5\ \{\ print\ n\ ;\ n=n+1\ ;\ k\ 0\ \} $$]
Evalúo el [$ if $] que, al ser cierto, es igual a evaluar su cuerpo.
[$$ print\ n\ ;\ n=n+1\ ;\ k\ 0 $$]
Como [$ n $] valía [$ 0 $], imprimimos un cero.
[$$ n=n+1\ ;\ k\ 0 $$]
Y [$ n $] vale [$ 1 $]
[$$ k\ 0 $$]
Ahora empieza el baile. Debido a que [$ k $] vale la continuación [$ \#\ []\ ;\ if\ n<5\ \{\ print\ n\ ;\ n=n+1\ ;\ k\ 0\ \} $], evaluamos a:
[$$ (\#\ []\ ;\ if\ n<5\ \{\ print\ n\ ;\ k\ 0\ \})\ 0 $$]
Aplicar la continuación es sustituir toda la expresión por la continuación sustituyendo el hueco por el operando evaluado (ya lo está, es el cero).
[$$ 0\ ;\ if\ n<5\ \{\ print\ n\ ;\ k\ 0\ \} $$]
El cero se ignora en la secuencia y repetimos el bucle con [$ n $] igual a [$ 1 $]. Obviamente, cuando sea [$ 5 $], el cuerpo del [$ if $] no se ejecutará y terminaremos el programa.
miércoles, 27 de octubre de 2010
Arreglado el LaTeX
lunes, 25 de octubre de 2010
miniSL parte 3 - Celdas
- Escaneador: Caracteres a tokens.
- Reconocedor: Tokens a AST.
- Generador: AST a código intermedio (o máquina).
- Ejecución: Código intermedio (o máquina) a valores de resultado.
Llamaremos valor a los posibles resultados de la evaluación de cierto código (código=AST). En principio, sólo podremos evaluar el código aunque existen valores que son código y se evalúan a ellos mismos: los literales como el entero 3 o la cadena "hola". Las celdas de valor entero serán del tipo INT_VAL y las cadenas STRING_VAL.
Es probable que necesitemos alguna celda especial de gestión del propio intérprete y que no será ni código ni valor (por ejemplo, una celda sin usar UNUSED). También (y coincidiendo con el LISP) tomaremos el constructor de lista (CONS_CTOR) como código y valor, aunque no es literal ya que lo evaluaremos. Así que, por ahora lo que tendría sería la siguiente clasificación de tipos de celdas.
enum CELL_TYPE
{
UNUSED,
//Literals
INT_VAL, STRING_VAL,
//Value constructors
//Code constructors
//Value and code constructors
CONS_CTOR,
};
Para terminar de rellenar esta lista de tipos de celda necesitamos saber cómo construir código y eso requiere conocer la sintaxis. Por eso la siguiente entrada de esta serie se dedicará a elegir una sintaxis para nuestro lenguaje script.
lunes, 18 de octubre de 2010
miniSL parte 2 - Pasos a realizar
- Escaneador (lexer): Leer los caracteres del código fuente y agruparlos en tokens. Los tokens son grupos de caracteres que tienen significado sintáctico. Es usual que el espacio en blanco y los comentarios se ignoren al buscar tokens. También es usual que se realicen ciertas transformaciones como calcular el valor de un número a partir de los caracteres que lo componen.
- Reconocedor (parser): Usando la sintaxis, reconstruir el árbol sintáctico del código fuente. Este paso es el reconocimiento y, debido a la simplicidad que queremos en nuestra implementación, en él utilizaremos una sintaxis con una gramática muy fácil de reconocer. En concreto, como veremos más adelante, será una sintaxis LL(1).
- Generación de código: Opcionalmente, se puede transformar el árbol sintáctico abstracto en el árbol objetivo abstracto y generar código a partir de él. Este código podrá ser primero un código intermedio a ejecutar en una máquina virtual o a compilar en código máquina y ejecutar en una máquina real. En nuestro lenguaje miniSL no utilizaremos esta transformación y ejecutaremos directamente el árbol sintáctico por simplicidad.
- Ejecución: La ejecución del resultado de los pasos anteriores. Esto podrá ser o bien la ejecución del árbol sintáctico, o bien la ejecución en una máquina virtual de un código intermedio generado por el paso 3, o bien la ejecución en una máquina real del código máquina generado por el paso 3. Existe la posibilidad de realizar el paso 3 mientras se ejecuta. Esto ya se comentó en una entrada anterior.
miércoles, 13 de octubre de 2010
miniSL parte 1
- En LISP se escribe: (+ (* 5 2) x)
- Lo que usualmente se escribe como: 5*2+x
De estas ideas surge miniSL ("mini scripting language" o "mini lenguaje de script") que, en poco más de mil líneas de código C++, implementa un lenguaje con las siguientes características destacables:
- Sintaxis no trivial con operadores prefijos, infijos y postfijos.
- Sentencias de control de selección (if) y bucle (while).
- Recolección de basura.
- Manejo explícito de entornos (let).
- Funciones anónimas (funciones lambda).
- Bucle REPL.
- Varios tipos de datos básicos: booleano, entero y cadena.
- Distinción entre declaración y modificación de variables.
- Posibilidad de definición de funciones nativas adicionales.
martes, 5 de octubre de 2010
Enlaces de interés
jueves, 30 de septiembre de 2010
El isomorfismo de Curry-Howard
Historia
Todo empezó cuando, en 1934, Haskell Curry se fijó en lo siguiente:
Si tengo una función f que toma un valor de tipo A y devuelve un valor de tipo B, su tipo lo escribiré como A -> B. Para indicar que f tiene ese tipo usaré los dos puntos f : A -> B y leeremos "f tiene tipo función de A a B". Escribiré los tipos en mayúsculas y los términos en minúscula. Para aplicar esa función a un término t arbitrario uso la siguiente regla de inferencia:
Si sé que f : A -> B y sé que t : A entonces puedo deducir que f(A) : B.
El golpe de genialidad de Curry consistió en quitar los términos y observar que los tipos solos conforman la regla de inferencia lógica del modus ponens.
Si sé que A implica a B y sé que A es cierto, entonces puedo deducir que B es cierto.
Tras años de trabajo, en 1958, Curry concluyó que no podía expresar la lógica proposicional clásica. Sólo una parte de ella llamada lógica intuicionista. En esta lógica no tenemos el principio del tercero excluido por lo que no podemos realizar demostraciones por reducción al absurdo.
Años más tarde, William Alvin Howard descubrió que no sólo se podía expresar la lógica proposicional intuicionista, sino un gran conjunto de lógicas intuicionistas incluidas las de primer orden y orden superior. Desde entonces se ha extendido aún más la correspondencia y se ha incluido la lógica clásica mediante el uso de continuaciones. De hecho, se han inventado lógicas gracias a la correspondencia.
Explicación
¿Pero cómo es posible que un tipo sea una proposición lógica? En todo caso un tipo es un conjunto de valores o de términos, pero ¿cómo expresar conjunciones o implicaciones? Aunque no lo parezca a primera vista, es relativamente fácil.
Por ejemplo, ¿qué significa cuando decimos 3 : int ? Que tres es un entero, sí. Pero también podemos decir que los enteros tienen algún habitante: existe un valor, el 3, que es un entero y por tanto los enteros no están vacíos. En este sentido el valor 3 sería la demostración de que los enteros están habitados. La proposición int significa "los enteros están habitados". Si nuestro lenguaje de programación no tuviera enteros, int sería falso. Si los tiene, int es cierto.
Entonces, los términos son, por un lado, valores de un tipo y, por otro, demostraciones de que ese tipo no está vacío. Que un tipo no esté vacío significa que, visto como proposición, tiene una demostración y por tanto es cierto en nuestro sistema o lenguaje de programación.
Seguimos: ¿Cómo demuestra una función una implicación? Viendo la regla modus ponens de arriba, la demostración de que B está habitado es f(t) así que lo que hace una función f es, dada una demostración t, construye otra f(t). O como siempre se ha entendido, dado un valor devuelve otro. Por esta razón demuestra la implicación: dame una demostración de A que te doy otra de B. Si A es cierto, entonces B también.
Hasta ahora tengo predicados constantes como int e implicaciones como A->B. Introduciremos la conjunción A & B. Desde el punto de vista lógico si A & B es cierto es por que A es cierto y B es cierto. Si me pongo a trabajar con las demostraciones necesito la demostración de A y la demostración de B para tener la demostración de A & B. Llamemos a estas demostraciones a : A y b : B. Entonces, un término que agrupa ambas demostraciones es un par (a, b). Por tanto, el tipo conjunción no es más que el tipo de los pares (a, b) : A & B más usualmente llamado producto cartesiano.
De esta forma se pueden obtener todas las conectivas en gran cantidad de lógicas distintas y, lo que es más importante, se estandariza la forma de demostrar las proposiciones en dichas lógicas: Los programas son esas demostraciones.
 |
| Portada de las actas del congreso LICS'90, humorísticamente titulada el homeomorfismo de Curry-Howard. Los constructores de tipos (arriba) se transforman en las conectivas lógicas (abajo) de forma continua. |
Para finalizar vamos a demostrar, usando programas como prueba, que A -> B -> C es lógicamente equivalente a (A & B) -> C. Para esto primero demostraremos ( (A & B) -> C) -> (A -> B -> C) y luego (A -> B -> C) -> ( (A & B) -> C).
λ f. (λ x. λ y. f (x, y) ) : ( (A & B) -> C) -> (A -> B -> C)
λ f. λ x. f (primero x) (segundo x) : (A -> B -> C) -> ( (A & B) -> C)
Sólo hay que hacer notar que hemos usado las proyecciones de un par: primero (p, q) se evalúa a p y segundo (p, q) se evalúa a q. El resto de la demostración es obvia en el sentido de que el programa que proporciono tiene ese tipo que digo. Para comprobar eso harían falta ciertas reglas de inferencia, pero eso será para otro día.
sábado, 25 de septiembre de 2010
Implementando el algoritmo de la playa de agujas
Antes de entrar de lleno en materia, hemos de explicar las funciones y tipos auxiliares que vamos a usar.
- RESULTADO: El tipo del resultado del algoritmo. Será una expresión parentizada como 1+(2*3).
- TOKEN: El tipo de los elementos de la entrada podrán ser o bien operandos simples como 1, 2 o 3; o bien operadores como +, * o -.
- PrioridadDelOperador(t): Si t es un TOKEN de tipo operador, devuelve su prioridad. Los operadores con más prioridad se agrupan antes que los de menos prioridad.
- ElSiguienteTokenEsOperador(): Devuelve cierto si el siguiente TOKEN a leer es un operador.
- LeeOperandoSimple(): Lee de la entrada un operando simple y lo consume quitándolo de la entrada. Falla (y el algoritmo termina con error) si el siguiente TOKEN es un operador.
- ConsultaSiguienteToken(): Lee sin consumir el siguiente TOKEN de la entrada.
- ConsumeToken(): Consume el siguiente TOKEN de la entrada quitándolo de la misma.
- CreaExpresion(operador, operando1, operando2): Crea una expresión parentizada con los operadores y operandos dados. Así, por ejemplo, CreaExpresion(+, 3, 7-2) crea la expresión 3+(7-2).
RESULTADO LeeExpresion(int pri_anterior)
{
RESULTADO a=LeeOperandoSimple();
if(!ElSiguienteTokenEsOperador())
return a;
TOKEN t=ConsultaSiguienteToken();
int pri_siguiente=PrioridadDelOperador(t);
if(pri_siguiente<pri_anterior)
return a;
ConsumeToken();
return CreaExpresion(t.data, a, LeeExpresion(prec));
}
Esta implementación funciona muy bien cuando todos los operadores son asociativos por la derecha. Es decir, tendremos que 1+2+3+4 se agrupa como 1+(2+(3+4)). Si queremos operadores que se asocien por la izquierda, necesitamos modificar ligeramente el algoritmo. También necesitamos saber si un operador es asociativo por la derecha o no. Esto lo conoceremos usando OperadorEsAsociativoDerecha(t) donde t es un TOKEN.
Este algoritmo mejorado es el siguiente:
RESULTADO LeeExpresion(int pri_anterior)
{
RESULTADO a=LeeOperandoSimple();
while(ElSiguienteTokenEsOperador())
{
TOKEN t=ConsultaSiguienteToken();
int pri_siguiente=PrioridadDelOperador(t);
if(OperadorEsAsociativoDerecha(t) ? pri_siguiente<pri_anterior : pri_siguiente<=pri_anterior)
return a;
ConsumeToken();
a=CreaExpresion(t.data, a, LeeExpresion(prec));
}
return a;
}
Usando estos algoritmos es muy sencillo añadir operadores infijos a un reconocedor descendiente recursivo.
lunes, 20 de septiembre de 2010
Fallo de LaTeX
Intensión y extensión
Todo par de conjuntos que contengan elementos iguales son conjuntos iguales.En el caso de la computación, lo que tendríamos sería
Toda par de funciones cuyos resultados para cualquier entrada sean los mismos son funciones iguales.Algo más matemáticamente sería decir que para todo
[$$ x $$]
si
[$$ f x =_\beta g x $$]
entonces
[$$ f =_{\beta\eta} b $$]
Lo interesante es que en el primer igual, con subíndice beta, estamos únicamente usando las definiciones y no la extensionalidad. Cuando usamos sólo las definiciones decimos que trabajamos intensionalmente. El segundo igual es distinto porque hemos usado la extensionalidad.
Lo más interesante de todo esto es que basta añadir la regla eta para que la igualdad intensional se convierta en extensional en el lambda cálculo. El problema es que esa simple regla introduce muchos quebraderos de cabeza a la hora de demostrar las propiedades de los sistemas que la usan.
La idea es bien sencilla. Como
[$$ f x $$]
se puede obtener mediante una beta-conversión desde
[$$ (\lambda y.f y) x $$]
y puedo decir que
[$$ f x =_\beta (\lambda y.f y) x $$]
Al aplicar extensión obtengo que
[$$ f =_{\beta\eta} \lambda y. f y $$]
Tomando la dirección que simplifica la expresión obtengo la eta-regla (como la variable que introduzco es fresca, no debe aparecer en f para poder aplicar la regla).
[$$ \lambda x. f x \rightarrow f $$]
Basta añadir esta regla para comprobar si dos funciones son iguales (aunque se hayan definido de forma distinta). Esto no es inmediato ya que existen teoremas bien profundos para este tipo de igualdades extensivas. Afortunadamente la simplicidad del lambda cálculo permite automatizarlo (aunque recordemos que el lambda cálculo sin tipos puede no acabar la computación).
Resumiendo: tenemos tres tipos de igualdades.
- Igualdad sintáctica. Dos términos son iguales si son el mismo. En el lambda cálculo hay cierto detalle y es que las variables se pueden renombrar. Esto es a lo que se llama la alfa-conversión. Llamamos entonces a los términos iguales sintácticamente alfa-equivalentes.
- Igualdad intensional. Dos términos son iguales si, sustituyendo sus definiciones, son el mismo. En el lambda cálculo esto se consigue aplicando la regla beta. Por esta razón se llaman términos beta-equivalentes (aunque también son alfa-equivalentes y deberían llamarse alfa-beta-equivalentes).
- Igualdad extensional. Dos términos son iguales si hagamos lo que hagamos con ellos obtenemos el mismo resultado siempre. Se obtienen usando las reglas beta y eta. Por esta razón se llaman beta-eta-equivalentes (aunque también se use la alfa-conversión).
[$$ (\lambda x.\lambda y. x) 3 = \lambda y. 3 $$]
[$$ \lambda x.x = \lambda y.y $$]
[$$ \lambda x. 5*(x+2) = \lambda x. 5*x+10 $$]
miércoles, 15 de septiembre de 2010
La transformación de Smirnov
Existen varios métodos, algunos con nombres tan bellos como el algoritmo del zigurat. Nos quedaremos con el más simple y versátil, aunque no siempre el más eficiente o exacto.
El procedimiento es bien simple. Si queremos generar una variable pseudoaleatoria con una densidad de probabilidad f, lo primero que necesitamos es calcular su distribución de probabilidad F. Esto es, básicamente, calcular una integral. Muchas veces no será posible analíticamente, razón por la cual este método no se puede usar siempre o requiere un cálculo numérico que deteriora la eficiencia del mismo.
Supongamos que podemos calcular la distribución de probabilidad F. En este caso el método consiste en transformar la variable pseudoaleatoria uniforme que hemos generado, normalizada entre cero y uno, usando la inversa de la distribución de probabilidad.
 |
| A la izquierda, la distribución de probabilidad. A la derecha su inversa. Cabe notar que los intervalos uniformes en el eje de abscisas se transforman en intervalos que siguen la densidad de probabilidad deseada en el eje de ordenadas. |
Este método es llamado la transformación de Smirnov (nada que ver con el vodka) o, el método de la inversa de la transformada.
domingo, 5 de septiembre de 2010
Estadísticas de la red
jueves, 26 de agosto de 2010
La maldición del programador
- Me había dado toda la información del protocolo serie para controlar la cámara de vídeo.
- Él había sido programador durante años y sabía lo que costaba hacer el programa. Literalmente me dijo "te hago un GUI en unos minutos".
- No podía cobrarle la depuración porque no sabía, por anticipado, qué fallos iba a haber en el programa (o si iba a haberlos).
- Podía usar los recursos que él tenía en su nave industrial. No necesitaba nada para programar, aparte del ordenador.
- El programa era muy pequeño y "en un rato se hacía".
- Después de estudiar y entender el protocolo serie (por cierto, no estándar) que me dio, descubrí que era otro protocolo el que realmente necesitaba ya que había un dispositivo "adaptador inteligente" que traducía de un protocolo a otro. A esta conclusión no llegué de inmediato sino que tuve que estar bastantes horas investigando. Además, esta investigación no fue a vuelapluma. Tuve que recurrir a conocimientos que me ha costado muchos años y esfuerzo tener. Por mucho menos un electricista te cobra un buen monto. Ni que decir tiene que, para poder hacer el presupuesto, tuve que estudiarme este segundo protocolo (por cierto, tampoco estándar).
- Yo también hago un GUI, no en minutos, en segundos. Cojo un lápiz y un papel y te dibujo unos cuadraditos que son los botones. Ya está. Claro que quizás él se refería a usar un programa donde pones los botones y con una opción te genera el código. Bueno, "el código" es sólo para poner los botones, nada de la lógica que hay detrás. Porque no querrá nadie que la cámara haga zoom cuando pulses el botón de apagado o que te diga que la cámara está encendida cuando no hay cámara conectada o que intente contactar por un puerto cuando está conectada a otro. Tampoco querrá nadie que no mande los checksums en el protocolo, que no respete la temporización o que ignore las respuestas del dispositivo diciendo que no está preparado para nuevas instrucciones. Y todo eso hay que programarlo y probarlo. Así que no es GUI todo el programa. De hecho, la mayor parte del programa es la lógica de control. Aunque no se vea. Es más, como no se ve, es la realmente difícil de programar y probar.
- Jamás he escrito un programa de más de 1000 líneas que no tuviera un fallo. Es verdad que la gran mayoría de fallos son tontos y, o bien los descubre el compilador, o bien los descubres rápidamente al ejecutar. Esto es cierto, pero también tiene una cara negativa: los errores que no descubres rápidamente son los difíciles. Los que ocurren al azar. Los que se detectan haciendo una operación en concreto tras haber hecho cinco antes de una forma dada. Los que no se ven, pero están. Y, en definitiva, los que más calentamientos de cabeza dan. A todo esto hay que añadir, en el caso de este cliente, que cada error que se descubra implica tener que coger el coche, ir a su nave, ver el problema y trabajar en campo. Hasta los fontaneros cobran los desplazamientos, ¿no?
- De hecho, no necesito nada para programar. No necesito ni el ordenador, me basta el cerebro. Los grandes programadores, los programadores muertos, escribían sus programas en papel. Concretamente, el papel de la revista en el que lo publicaban. Pero volvamos al mundo real. En un trabajo manual liberas tu mente. Si estás apretando tuercas y pensando en la vecina del segundo no creo que tu trabajo se vea afectado. Esto no ocurre con la programación. En la programación tienes que pensar el programa. Si dejas de pensar en el programa, no avanzas. Es más, suele ocurrir lo contrario. Suele ocurrir que dejas de programar, te vas, no sé, a comer y ¡sigues pensando en el programa! Estoy viendo la tele ¡trabajando! De paseo, ¡trabajando! En la ducha, ¡trabajando! ¿Cuento o no cuento esas horas de trabajo? Y lo digo en serio porque la ducha es unos de mis momentos más productivos, cuando se me ocurren las mejores ideas de diseño que simplifican un programa drásticamente. ¿Y ahora, qué hacemos?
- Esto se relaciona con el punto 2. El famoso "yo fui programador aficionado". Esta frase deja entrever que "y programar es divertido". No te voy a pagar por algo que, si te diviertes, no es trabajo. Bueno, es que hay una diferencia, yo llevo 26 años programando y llega un momento en el cual no te divierte tanto. En el cual, es un trabajo. El problema es que el programador aficionado se pone con el ordenador y se divierte. Se le pasan las horas y cree que ha sido menos tiempo. Así que cuando dice "en un rato se hace" no tiene en cuenta que su visión de la programación está sesgada. Su "rato" fue en realidad de muchas horas. Claro que, con el tiempo, sólo se recuerdan las cosas agradables. Un rato agradable.
domingo, 22 de agosto de 2010
Divide para sumar
Aritmética modular
La aritmética modular surge cuando trabajamos con los restos (o residuos) de una división con un divisor (o módulo) dado. Así, el residuo de 7 dividido entre (módulo) 3 es uno ya que 7=3·2+1. El teorema de la división nos indica que este valor existe y es único.
Los distintos lenguajes de programación incluyen tanto una operación de división como una operación de obtener el residuo. En la familia del C, se nota con el símbolo %.
Resulta que bajo un módulo dado, las operaciones de suma y multiplicación forman un anillo conmutativo. En todo caso, nos interesa la siguiente identidad
(a·b)%m == [(a%m)·(b%m)]%m
Bits y bytes
Por otra parte, cuando un número se almacena en base dos, cada bit se pondera a una potencia de dos. Esto es básico.
1001 = 1·8 + 0·4 + 0·2 + 1·1 = 9
Pero, ¿qué ocurre si obtengo el residuo de un número así? Probemos a hacer 9%7. El resultado es obviamente 2, pero ¿qué ocurre en las ponderaciones de bits?
9%7 = [1·(8%7) + 0·(4%7) + 0·(2%7) + 1·(1%7)]%7 = [1·1 + 0·4 + 0·2 + 1·1]%7 = 2%7 = 2
Es interesante ver que el bit que está con ponderacion 8 ahora pondera 1. Así que lo que estamos obteniendo es la suma de los dígitos octales módulo siete. Es decir, con números octales es fácil de calcular el resto módulo siete. Ejemplo:
0376252%7 = (3+7+6+2+5+2)%7 = 25%7 = 4
Si en vez de usar 7 usamos otro módulo, estaremos contando los dígitos en la base del siguiente número. En los números decimales tendríamos que usar módulo 9 y lo que obtenemos no es más que el criterio de divisibilidad por nueve: suma cifras y que éstas sean divisibles por nueve.
Divide para sumar
Ahora podemos utilizar este truco para sumar los bytes de un entero.
0xXXYYZZWW % 255 = (0xXX+0xYY+0xZZ+0xWW)%255
Siempre y cuando no llegue la suma a 255, la suma es exacta. Si fuera necesario sumar más de 255, se usarían operaciones AND y desplazamientos. Se separa el número en dos, se suman dividiéndolos con módulo 65535 y luego se suman los resultados parciales. Algo más tedioso pero que se rentabiliza si de todas las maneras hay que hacer estas operaciones como ocurre en muchos algoritmos que trabajan con bits.
martes, 17 de agosto de 2010
Contando alteraciones
Escalas, clases de tono y rotaciones binarias
En la música usual se trabaja con doce clases de tono. Es fácil ver que las teclas de un piano repiten su distribución cada doce (siete blancas y cinco negras). De estas doce clases de tono, una escala es un subconjunto de ellas. Representaremos a este conjunto con doce bits. A cero si no está en el conjunto a uno si está.

Por ejemplo, empezando en un DO, las teclas blancas del piano son 101011010101 y las teclas negras (obviamente) su complementario 010100101010. Aquí tenemos nuestras dos primeras escalas: La escala diatónica mayor natural y la escala pentatónica.
La escala mayor, como la hemos empezado en DO, tiene esa tonalidad y por eso es usual decir que es la es cala de DO mayor. Si por ejemplo quisiéramos la escala de RE mayor, deberíamos empezar por la nota RE que está dos teclas a la derecha (dos semitonos y en nuestra notación dos bits) del DO. Sería algo como 00101011010101.
Entonces tenemos catorce bits, y eso no puede ser porque sólo tenemos doce clases de tono. Lo que ocurre es que las clases de tono son cíclicas y por tanto la operación correcta para pasar de la escala en tonalidad de DO a tonalidad de RE es la rotación y no el desplazamiento de bits. Entonces, en vez de poner 00101011010101, rotamos a 011010110101.
Alteraciones, movimiento de bits y distancia
Ahora bien, las escalas musicales tienen una propiedad que se denomina máxima uniformidad. Esto significa que rotar la escala la cambia poco. De hecho, si comparamos la escala en DO (rotación 0) y la escala en RE (rotación de 2 bits) sólo hemos movido dos unos.
101011010101
011010110101
Mover un 1 en esta representación equivale a realizar una alteración musical. Existen dos tipos de alteraciones: sostenido si movemos el uno a la derecha (como en este ejemplo) o bemol si lo movemos a la izquierda. (Nota: Aquí consideramos que doble bemol son dos bemoles y doble sostenido dos sostendios)
Es sensato pensar en definir una distancia entre estas dos tonalidades de la escala mayor. En este ejemplo la distancia sería de dos sostenidos. Ahora queda el problema de definir el algoritmo que obtenga esta distancia.
El algoritmo
Un detalle importante es que si dos unos coinciden, pueden asumirse como no alterados. Por ejemplo:
01100
00110
Es igual pensar en mover cada 1 un bit a la derecha o pensar que el uno común no se mueve y se mueve el primero dos lugares a la derecha. El resultado es siempre el mismo: dos sostenidos.
La primera intención es usar un XOR (diferencia simétrica), pero hemos de saber si movemos a la izquierda o a la derecha por lo que mantendremos un signo.
01100
00110
0+0-0 //XOR con signo
El + significa que ahí hay un 1 a mover a la derecha y el - que hay un 1 a mover a la izquierda. Ahora hemos de contar el número de unos a mover y luego el número de posiciones a mover.
01100
00110
0+0-0 //XOR con signo
01100 // Número de unos que se mueven en cada bit
01222 // Suma de lo de arriba: Número total de posiciones movidas.
Finalmente, para contar sostenidos y bemoles, es mejor llevar dos acumuladores por separados.
011000110
001101100
0+0-0-0+0 //XOR con signo
011000000 // Número de unos que se mueven A LA DERECHA (sostenidos)
000001100 // Número de unos que se mueven A LA IZQUIERDA (bemoles)
012222222 // Suma de sostenidos.
000001222 // Suma de bemoles
Distancia total: 2 sostenidos + 2 bemoles = 4 alteraciones
Caminos conocidos y desconocidos
Si nos ponemos a calcular las distancias entre escalas encontramos algo conocido: el círculo de quintas. El círculo de quintas nos da la distancia entre dos tonalidades distintas de escalas mayores (o menores).
Existen otras escalas exóticas como la mayor doble armónica o la escala alterada cuya distancia no aparece en el círculo de quintas. En este caso el algoritmo de arriba nos dice que, por ejemplo, entre SOL menor y MI mayor doble armónica la distancia es
101101010110 //SOL menor
100111001101 //MI mayor doble armónica
00+0-00+-0+- //XOR con signo
001100010010 //Movimiento de sostenidos
000000000000 //Movimiento de bemoles (no hay)
001222233344 //Sostenidos 4
Así que hay una distancia de cuatro sostenidos.
La única limitación del algoritmo es el número de bits puestos a uno, que debe ser igual en las escalas a comparar. A fin de cuentas, el algoritmo mide alteraciones, y si no hay un bit a uno, no hay nada que alterar.
viernes, 13 de agosto de 2010
Otra chuchería binaria
Sigo buscando y encontrando algoritmos curiosos para manipular bits. Éste cuenta el número de bits puestos a uno. Es decir, el peso de Hamming. Realmente hay muchísimas variantes y mejoras, pero esta es la más elegante desde mi punto de vista.
int bitcount (unsigned int n) {
int count = 0 ;
while (n) {
count++ ;
n &= (n - 1) ;
}
return count ;
}
sábado, 24 de julio de 2010
Relaciones binarias

Para ver bien los detalles es mejor usar este pdf.
domingo, 18 de julio de 2010
Selección con el preprocesador
Después de hablar de las macros hace unos días, me he dedicado a investigar algo más sobre cómo funciona el preprocesador de C/C++. Está muy limitado, pero tiene algunas posibilidades.
Usando #if/#endif es posible seleccionar parte de código, pero no podemos usar #if/#endif dentro de una macro. Es decir algo como esto no funciona
#define SELECCIONA(a,b,c) #if a \
b \
#else \
c \
#endif
El motivo es que el preprocesador es muy tonto y sus comandos (que empiezan por #) sólo son reconocidos a principio de línea. Debido a que el \ a final de línea significa que se sigue en la siguiente línea como si fuera esta, la macro anterior sería equivalente a
#define SELECCIONA(a,b,c) #if a b #else c #endif
Por lo que ni el #if ni el #else ni el #endif son reconocidos como comandos de preprocesador.
La solución es algo enrevesada, pero funciona y es usada en boost::preprocesor. Se basa en el concatenador de tokens. Es un operador especial (no es un comando) del preprocesador. Se escribe ##. El resultado de esta concatenación es agrupar dos identificadores en uno.
#define CONCATENA(a,b) a ## b
CONCATENA(hola, adios) //Equivalente a escribir holaadios
Debido a que el preprocesador vuelve a expandir el resultado de sus macros, es fácil usar el siguiente truco para la selección.
#define IF_TRUE(t,e) t
#define IF_FALSE(t,e) e
#define IF(c,t,e) IF_##c (t, e)
IF(TRUE, bien, mal) //Se expande a IF_TRUE(bien,mal) y se vuelve a expandir a bien
Ahora podemos combinar este truco con la técnica explicada hace unos días para crear código opcionalmente.