jueves, 26 de mayo de 2011
lunes, 23 de mayo de 2011
miniSL parte 13 - El entorno global
En la parte anterior de esta serie hablamos del entorno global como conjunto raíz del recolector de basura. El código relacionado está en la parte octava de esta serie, en la función GarbageCollect(). También dijimos que el entorno global no es más que una celda destacada.
Lo importante es que m_GlobalEnvir no va a cambiar y siempre va a ser un entorno. Vimos la función CreateEnvir() en la parte 11. En la parte 6 explicamos que una celda de entorno (de tipo ENVIR_VAL) sólo tiene un puntero a una tabla hash o árbol de búsqueda así que, como lo que vamos a hacer con este entorno es definir símbolos en él, sera muy útil obtener directamente la tabla del entorno global.
Antes nos vamos a dedicar a la evaluación, puesto que tenemos ya especificado todo lo que hace falta para explicarla.
CELL* m_GlobalEnvir;La creación de esa celda se va a realizar cuando iniciemos todo el sistema del lenguaje script. En el constructor de la clase Script.
Script() : m_FirstUnused(NULL) { m_GlobalEnvir=&CreateEnvir(NULL); }Recordemos que m_FirstUnused se usaba para reutilizar las celdas recicladas por el recolector de basura.Lo importante es que m_GlobalEnvir no va a cambiar y siempre va a ser un entorno. Vimos la función CreateEnvir() en la parte 11. En la parte 6 explicamos que una celda de entorno (de tipo ENVIR_VAL) sólo tiene un puntero a una tabla hash o árbol de búsqueda así que, como lo que vamos a hacer con este entorno es definir símbolos en él, sera muy útil obtener directamente la tabla del entorno global.
ENVIR_TABLE& GlobalEnvirTable()const { return *m_GlobalEnvir->envir_table; }La mayor parte de símbolos que vamos a definir en la tabla del entorno global son operaciones nativas. La función DefineGlobalNative() nos ahorra tener que llamar a CreateName() y CreateNative() cada vez.void DefineGlobalNative(STRING const& name, NATIVE nat)
{
(*m_GlobalEnvir->envir_table)[&CreateName(name)]=&CreateNative(nat);
}Finalmente, poblaremos la tabla del entorno global con la función DefineUsualSymbols(). Se declara así en la clase Script.void DefineUsualSymbols();Y se define así.
void Script::DefineUsualSymbols()
{
DefineGlobalNative(L"=", &Native_Set);
DefineGlobalNative(L"+", &Native_Add);
DefineGlobalNative(L"-", &Native_Sub);
DefineGlobalNative(L"*", &Native_Mul);
DefineGlobalNative(L"&", &Native_BAnd);
DefineGlobalNative(L"|", &Native_BOr);
DefineGlobalNative(L"^", &Native_BXor);
DefineGlobalNative(L"/", &Native_Div);
DefineGlobalNative(L"%", &Native_Mod);
DefineGlobalNative(L"==", &Native_Eq);
DefineGlobalNative(L"!=", &Native_Ne);
DefineGlobalNative(L"<", &Native_Lt);
DefineGlobalNative(L"<=", &Native_Le);
DefineGlobalNative(L">", &Native_Gt);
DefineGlobalNative(L">=", &Native_Ge);
DefineGlobalNative(L"if", &Native_If);
DefineGlobalNative(L"let", &Native_Let);
DefineGlobalNative(L"while", &Native_While);
DefineGlobalNative(L"begin", &Native_Begin);
DefineGlobalNative(L"define", &Native_Define);
DefineGlobalNative(L"set", &Native_Set);
DefineGlobalNative(L"lambda", &Native_Lambda);
(*m_GlobalEnvir->envir_table)[&CreateName(L"true")]=&CreateBool(true);
(*m_GlobalEnvir->envir_table)[&CreateName(L"false")]=&CreateBool(false);
}La mayoría de estas funciones nativas (hemos prefijado el nombre con Native_ para distinguirlas claramente) todavía no están definidas. Lo haremos en las partes de la 26 a la 31.Antes nos vamos a dedicar a la evaluación, puesto que tenemos ya especificado todo lo que hace falta para explicarla.
Etiquetas:
miniSL
miércoles, 11 de mayo de 2011
El punto de la pereza
Hace unos días Bob Harper, que defiende SML con uñas y dientes, se dedicó a atacar a los elitistas del Haskell. Su idea era muy sencilla: los tipos de Haskell no son inductivos. Voy a intentar explicar esto de forma sencilla.
Tipos inductivos
Son los tipos cuyos valores se construyen con unos valores bases y unos constructores. El caso arquetípico son los números naturales.
Las listas de naturales son árboles con infinitas ramas ya que, cada vez que usamos un constructor con un natural distinto, generamos una nueva rama. Es difícil dibujar esto porque cada una de las infinitas ramas lleva a infinitos valores que, a su vez, vuelven a tener infinitas ramas. Con un poco de imaginación el diagrama sería algo así.
Existen también los llamados tipos coinductivos en los cuales, en vez de tener una lista vacía (valores base) y usar constructores sobre ella, tenemos una lista llena (valores co-base) y usamos destructores (co-constructores) sobre ella. No hablaré mucho más de esto aquí.
Evaluación perezosa
La evaluación perezosa, de la que hablamos alguna que otra vez, consiste básicamente en no evaluar hasta que no sea estrictamente necesario. Un caso clásico es la multiplicación por cero.
0*(7+5)
¿Para qué sumar siete y cinco si sabemos que al final la multiplicación va a ser cero? Bueno, existe un motivo por el que evaluar los argumentos y son los efectos laterales. Si en vez de sumar dos números imprimiésemos un mensaje, la cosa cambia.
0*(print "hola")
Ahora sí que habría que imprimir "hola" aunque el resultado de esta multiplicación (si es que print devuelve un número, claro) sea cero. Pues bien, ocurre que en Haskell no hay efectos secundarios. Es un lenguaje funcional. En este lenguaje de programación sí que conviene no perder tiempo evaluando cosas que, al final, no se van a usar.
La idea fundamental de la crítica de Harper es que siempre existen los efectos secundarios. En concreto existe un efecto secundario que jamás puedes quitarte de encima en un lenguaje de programación Turing completo. Ese efecto es... que la computación no termine.
Imaginemos el siguiente programa:
f(x) = 1+f(x) //Esta computación no termina
0*f(3)
Si el lenguaje es estricto y evalúa f(3), nunca llega a ejecutar la multiplicación. Si el lenguaje es perezoso y no evalúa f(3), la multiplicación ha aceptado un valor que no es un número (de hecho ni siquiera es un valor, es no terminación) y lo ha tratado como si fuera un número. ¿Cuál es el tipo del argumento que ha aceptado la multiplicación?
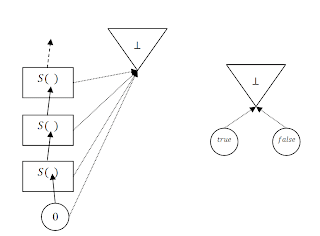
Los lenguajes con evaluación perezosa cuelan entre los valores de sus tipos la no terminación. O mejor dicho, algo todavía sin evaluar que puede ser no terminación o puede ser un valor concreto. Este valor tan especial que se puede convertir en otro (o no) se corresponde con el mínimo de un orden parcial completo con mínimo. Este mínimo tiene el nombre de "punto" y se suele representar con el símbolo [$\bot$].
Si añadimos el punto a los tipos inductivos el resultado es que ¡no son inductivos! Los naturales y los booleanos quedan algo así.
Epílogo
Por supuesto, esto es todo cuestión de compromisos. Usar evaluación perezosa abre la puerta a tener tipos coinductivos con mucha facilidad. De hecho la "lista llena" de la que hablé antes es precisamente el punto [$\bot$]. Una computación que puede no terminar, una lista infinita, de la cual vamos extrayendo valores, como los iteradores. Esto permite cosas nuevas como el uso de la composición en estos tipos coinductivos, lo que abre la posibilidad a la reutilización de código.
Tipos inductivos
Son los tipos cuyos valores se construyen con unos valores bases y unos constructores. El caso arquetípico son los números naturales.
- El 0 es un valor base.
- El siguiente número natural S(n), es un constructor que, dado un número, construye otro.
- El cero es 0
- El uno es S(0)
- El dos es S(S(0))
- Y así.
- La lista vacía [] es un valor base.
- El constructor de lista cons(V,R) toma un valor V de un tipo T y el resto de la lista R de tipo L(T).
- Tomamos la lista vacía [] como valor base de una lista de enteros L(int)
- Añadimos un entero cons(-3, [])
- Añadimos otro entero cons(7, cons(-3, []) )
 |
| Los booleanos son dos valores base: true y false. No hay constructores. Estos tipos sin constructores suelen llamarse tipos enumerados. |
Las listas de naturales son árboles con infinitas ramas ya que, cada vez que usamos un constructor con un natural distinto, generamos una nueva rama. Es difícil dibujar esto porque cada una de las infinitas ramas lleva a infinitos valores que, a su vez, vuelven a tener infinitas ramas. Con un poco de imaginación el diagrama sería algo así.
 |
| Lista de naturales. La lista vacía es el valor base [] que está abajo. A partir de él construimos infinitos valores, uno para cada natural. Serían las listas de un único natural. Asimismo, de cada uno de estos valores se obtienen otros infinitos valores. A este tipo de árboles infinitos pero con una estructura simple se los denomina árboles regulares. |
Existen también los llamados tipos coinductivos en los cuales, en vez de tener una lista vacía (valores base) y usar constructores sobre ella, tenemos una lista llena (valores co-base) y usamos destructores (co-constructores) sobre ella. No hablaré mucho más de esto aquí.
Evaluación perezosa
La evaluación perezosa, de la que hablamos alguna que otra vez, consiste básicamente en no evaluar hasta que no sea estrictamente necesario. Un caso clásico es la multiplicación por cero.
0*(7+5)
¿Para qué sumar siete y cinco si sabemos que al final la multiplicación va a ser cero? Bueno, existe un motivo por el que evaluar los argumentos y son los efectos laterales. Si en vez de sumar dos números imprimiésemos un mensaje, la cosa cambia.
0*(print "hola")
Ahora sí que habría que imprimir "hola" aunque el resultado de esta multiplicación (si es que print devuelve un número, claro) sea cero. Pues bien, ocurre que en Haskell no hay efectos secundarios. Es un lenguaje funcional. En este lenguaje de programación sí que conviene no perder tiempo evaluando cosas que, al final, no se van a usar.
La idea fundamental de la crítica de Harper es que siempre existen los efectos secundarios. En concreto existe un efecto secundario que jamás puedes quitarte de encima en un lenguaje de programación Turing completo. Ese efecto es... que la computación no termine.
Imaginemos el siguiente programa:
f(x) = 1+f(x) //Esta computación no termina
0*f(3)
Si el lenguaje es estricto y evalúa f(3), nunca llega a ejecutar la multiplicación. Si el lenguaje es perezoso y no evalúa f(3), la multiplicación ha aceptado un valor que no es un número (de hecho ni siquiera es un valor, es no terminación) y lo ha tratado como si fuera un número. ¿Cuál es el tipo del argumento que ha aceptado la multiplicación?
Los lenguajes con evaluación perezosa cuelan entre los valores de sus tipos la no terminación. O mejor dicho, algo todavía sin evaluar que puede ser no terminación o puede ser un valor concreto. Este valor tan especial que se puede convertir en otro (o no) se corresponde con el mínimo de un orden parcial completo con mínimo. Este mínimo tiene el nombre de "punto" y se suele representar con el símbolo [$\bot$].
Si añadimos el punto a los tipos inductivos el resultado es que ¡no son inductivos! Los naturales y los booleanos quedan algo así.
Epílogo
Por supuesto, esto es todo cuestión de compromisos. Usar evaluación perezosa abre la puerta a tener tipos coinductivos con mucha facilidad. De hecho la "lista llena" de la que hablé antes es precisamente el punto [$\bot$]. Una computación que puede no terminar, una lista infinita, de la cual vamos extrayendo valores, como los iteradores. Esto permite cosas nuevas como el uso de la composición en estos tipos coinductivos, lo que abre la posibilidad a la reutilización de código.
lunes, 2 de mayo de 2011
La multiplicación de Gauss
¿Cómo realizar una multiplicación compleja usando sólo tres productos reales?
La multiplicación usual requiere cuatro:
[$$ (a+bi)(c+di) = ac-bd + (ad+bc)i $$]
El truco lo descubrió Gauss por 1805
[$$ ac-bd = ac +bc -bc -bd = c(a+b) - b(c+d) $$]
[$$ ad+bc = ad +ac-ac +bc = c(a+b) +a(d-c) $$]
Como vemos, se reusa la multiplicación [$c(a+b)$].
Esto me lleva a recordar el algoritmo de Strassen para multiplicar matrices, pero ese es otro tema.
La multiplicación usual requiere cuatro:
[$$ (a+bi)(c+di) = ac-bd + (ad+bc)i $$]
El truco lo descubrió Gauss por 1805
[$$ ac-bd = ac +bc -bc -bd = c(a+b) - b(c+d) $$]
[$$ ad+bc = ad +ac-ac +bc = c(a+b) +a(d-c) $$]
Como vemos, se reusa la multiplicación [$c(a+b)$].
Esto me lleva a recordar el algoritmo de Strassen para multiplicar matrices, pero ese es otro tema.
Etiquetas:
algoritmos,
matemáticas
Suscribirse a:
Comentarios (Atom)