Las funciones elípticas de Jacobi
Las funciones elípticas de Jacobi son una generalización de las funciones trigonométricas. Hay doce funciones elípticas de Jacobi, pero sólo vamos a usar una que se llama [$cd$] y está relacionada con el coseno. Si bien el argumento de las funciones trigonométricas son ángulos, el argumento de las funciones elípticas de Jacobi es un valor [$u$] que no tiene una relación inmediata ni con los ángulos, ni áreas ni longitudes de arco.
 |
| Trigonometría en la elipse usando las funciones elípticas de Jacobi [$sd$], [$nd$] y [$cd$]. Hay más funciones elípticas de Jacobi, pero sólo nos será de utilidad la [$cd$]. |
El valor [$k^'$] se llama el comódulo elíptico y se relaciona con la excentricidad de la elipse [$k$], también llamada el módulo elíptico, de la siguiente forma. [$$ k^2+(k^')^2=1$$] Dependiendo de la excentricidad de la elipse sobre la que trabajemos las funciones de Jacobi cambian por lo que es usual presentarlas con dos argumentos.[$$cd(u,k),\ \ \ \ sd(u,k),\ \ \ \ nd(u,k)$$] En concreto, la función [$cd(u,k)$] es muy parecida al coseno cuando se observa su inversa. [$$ arccd(u,k)=\int_u^1{\frac{dt}{\sqrt{1-t^2}\sqrt{1-k^2 t^2}}}$$] Investigaremos el recorrido que hace esta función cuando [$u$] se mueve desde [$0$] hasta infinito. Empieza en [$$ arccd(0,k)=\int_0^1{\frac{dt}{\sqrt{1-t^2} \sqrt{1-k^2 t^2}}}$$] Este valor es conocido como la integral elíptica completa de primera especie de módulo [$k$] y se escribe usualmente como [$K(k)$].
 |
| Diagrama representando el valor real resultado de la integral completa de primera especie que es el valor del [$arccd$] de cero. |
Conforme aumente [$u$] por los reales, decrecerá el [$arccd$] hasta que lleguemos a [$u=1$] donde los límites de la integral van a coincidir por lo que su valor será cero. Si hacemos el recorrido simétrico hacia los valores negativos, llegaremos a [$u=-1$] donde el valor de su [$arccd$] será [$2K(k)$].
 |
| Recorrido del valor de [$arccd$] con argumentos desde cero hasta uno (y simétrico por los negativos). |
A partir de este punto, seguir integrando significa que la raíz [$\sqrt{1-t^2}$] va a resultar en valores imaginarios. Nuestro recorrido pasará a moverse verticalmente por la gráfica hasta que [$u=\frac{1}{k}$]. A partir de este valor, la raíz [$\sqrt{1-k^2 t^2}$] también se hace imaginaria. El valor del [$arccd$] en [$u=\frac{1}{k}$] es fácilmente calculable mediante un cambio de variables. [$$ arccd \left(\frac{1}{k},k\right)=\int_{\frac{1}{k}}^1{\frac{dt}{\sqrt{1-t^2}\sqrt{1-k^2 t^2}}}=\int_0^1{\frac{dt}{\sqrt{t^2-1}\sqrt{1-(k^')^2 t^2}}}=jK(k^' )$$] Trazando estos segmentos verticales del recorrido obtenemos el siguiente diagrama.
 |
| Recorrido del valor de [$arccd$] con argumentos desde cero hasta [$\frac{1}{k}$] (y simétrico por los negativos) |
 |
| Recorrido completo del valor de [$arccd$] con argumentos reales. |
Sabiendo que al seguir este recorrido sobre la función [$cd(u,k)$] debemos obtener la función identidad, ganamos perspectiva de cómo es la función [$cd(u,k)$].
Secciones de cd
Su diagrama de polos y ceros se presenta a continuación y observamos que tiene dos periodos. El usual de [$4K(k)$] que se correspondería con el [$2\pi$] de las funciones trigonométricas y otro imaginario de [$2iK(k^' )$] que aparece por esa segunda raíz cuadrada en la integral. La zona sombreada es la que se repite periódicamente tanto horizontal como verticalmente.
 |
| Diagrama de polos, ceros y valores destacados de [$cd$]. |
Como hicimos con la función coseno, vamos a ver cómo es la función [$cd(u,k)$] en las tres secciones del recorrido de [$arccd(u,k)$]. Recordemos que en estas rectas la función [$cd(u,k)$] es real.
 |
| Tres secciones de la función [$cd$] por las rectas que va a seguir su [$arccd$]. En estas rectas el valor de [$cd$] es real y se representa a su derecha. |
Para la rama negativa tenemos que [$$ cd(u+2K(k),k)=-cd(u,k)$$] Además, existe una propiedad de simetría entre [$cd(t,k)$] y [$cd(t+jK(k^' ),k)$] que usaremos más adelante. [$$cd(u+jK^' (k),k)=\frac{1}{k\ cd(u,k)}$$] En la DLMF podemos ver en 3D la función [$cd$] con sus polos bien distinguidos.
http://dlmf.nist.gov/22.3.F19.mag
La función racional elíptica
El lector astuto ya habrá imaginado que lo siguiente que vamos a hacer es [$$cd(n\ arccd(u ,k),k)$$] Como hicimos con los polinomios de Chebyshev, el recorrido del [$arccd$] queda ampliado [$n$] veces. Siguiéndolo, nos haremos una idea de cómo es esta función. Como antes, sólo seguiremos los valores positivos ya que los negativos son simétricos.
 |
| Recorrido de [$arccd$] ampliado tres veces sobre el diagrama de polos y ceros de [$cd$]. |
El resultado es una oscilación entre +1 y -1 en el primer segmento, otra oscilación entre 1 y 1/k en el segundo segmento y otra oscilación entre 1/k e infinito (cambiando de signo en cada infinito) en el tercer segmento.
 |
| Gráfica de la función [$cd(3\ arccd(x, k), k)$] con cada uno de los tramos coloreados. |
Esta función no nos sirve como función [$F^2 (\omega)$] porque tendría oscilaciones en la banda de paso.
 |
| La función anterior al cuadrado como intento de aproximación a [$F^2(\omega)$]. La banda de transición es muy ancha y tiene oscilaciones. |
Afortunadamente tenemos dos [$k$] a nuestra disposición, la del [$arccd$] que llamaremos [$k_a$] y la del [$cd$] que llamaremos [$k_c$]. Entonces, se define la función racional elíptica de la siguiente forma:[$$R_n (u,k_a,k_c )=cd\left(n\ \frac{K(k_c )}{K(k_a )} arccd(u ,k_a ),k_c \right)$$] La aparición del cociente [$\frac{K(k_c )}{K(k_a )}$] es necesaria para convertir el periodo real del [$arccd$] en el periodo real del [$cd$] que ahora son distintos al tener módulos distintos. Bueno, exactamente [$n$] veces ese periodo.
Por otra parte, ese n no lo queremos en el periodo imaginario. Querríamos tener [$$ R_n (u,k_a,k_c )=cd\left(\frac{K(k_c^' )}{K(k_a^' )} arccd(u ,k_a ),k_c \right)$$] ¡Y podemos tener ambas condiciones si elegimos con cuidado! [$$ n=\frac{K(k_a )K(k_c^' )}{K(k_a^' )K(k_c )} $$] De esta forma el recorrido queda multiplicado sólo en la dirección horizontal.
 |
| El recorrido que tomamos en la función elíptica racional con unos parámetros adecuados para que sólo se mueva medio periodo imaginario. |
La gráfica de esta función es como sigue. En ella aparece tanto la [$k_a$] como la [$k_c$] explícitamente.
 |
| Gráfica de la función elíptica racional con módulos [$k_a$] y [$k_c$] (y la [$n$] adecuada según se comentó arriba). |
Como ocurría con los polinomios de Chebyshev, esta función es real, aunque esta vez no puede expresarse como un polinomio ya que tiene polos (los infinitos). Debe expresarse como un cociente entre polinomios, de ahí que se llame función racional elíptica.
El filtro de Cauer
El filtro de Cauer o filtro elíptico es el que toma esa función racional elíptica como [$F(\omega)$]. La gráfica de su cuadrado es la que sigue.
 |
| La función racional elíptica como función [$F(\omega)$] de un filtro. |
Ajustando para que se cumplan los requisitos de un filtro tenemos que [$$ F^2 (\omega)=\epsilon_p^2 R_n^2 \left(\frac{\omega}{\omega_p} ,\frac{\omega_p}{\omega_s} ,\epsilon_p \epsilon_s \right)$$] Donde hemos usado [$$k_a=\frac{\omega_p}{\omega_s}$$][$$ k_c=\epsilon_p \epsilon_s$$]
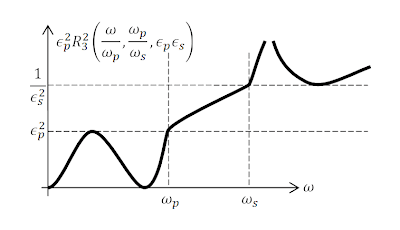 |
| La función racional elíptica como función [$F(\omega)$] de un filtro con los parámetros ajustados a las especificaciones del filtro. |
 |
| Respuesta en frecuencia de un filtro de Cauer |
Además, la condición de la no oscilación en la banda base y ajuste de periodos es precisamente la cota del orden del filtro. [$$ n\ge \frac{K(\frac{\omega_p}{\omega_s}) K^' (\epsilon_p \epsilon_s )}{K^' ( \frac{\omega_p}{\omega_s} )K( \epsilon_p \epsilon_s )}$$] Donde [$K^' (k)=K(k^' )$].
Ojo: una vez hallado [$n$] con la desigualdad, hemos de modificar algún requisito para que se cumpla la igualdad. Debemos tener la igualdad si no queremos oscilaciones en la banda de transición.
La búsqueda de la función de transferencia
Para obtener la función de transferencia necesitamos conocer los polos y los ceros de la misma. Ambos son sencillos de calcular. Hagamos el cambio [$\omega=-js$] y empecemos por los ceros de la función de transferencia. Ocurrirán cuando [$R_n^2$] tienda a infinito. Es decir, en los polos de [$R_n^2$]. [$$R_n^2 \left(\frac{-js_{cero}}{\omega_p} ,\frac{\omega_p}{\omega_s} ,\epsilon_p \epsilon_s \right)=\infty$$] [$$n \frac{K(\epsilon_p \epsilon_s )}{K(\frac{\omega_p}{\omega_s} )} arccd\left(\frac{-js_{cero}}{\omega_p} ,\frac{\omega_p}{\omega_s} \right)=arccd(\infty,\epsilon_p \epsilon_s )$$]
El miembro de la derecha es la localización de los polos de [$cd$]. Recordemos que hay dos periodos y, por la dirección del recorrido del [$arccd$] en la zona de los ceros, nos interesa el periodo real.[$$n \frac{K(\epsilon_p \epsilon_s )}{K(\frac{\omega_p}{\omega_s})} arccd\left(\frac{-js_{cero\ m}}{\omega_p} ,\frac{\omega_p}{\omega_s}\right)=(2m+1)K(\epsilon_p \epsilon_s )+jK^' (\epsilon_p \epsilon_s )$$]
Despejando llegamos a la expresión siguiente. [$$ s_{cero\ m}=j\omega_p cd\left(\frac{2m+1}{n} K\left(\frac{\omega_p}{\omega_s}\right)+jK^' \left(\frac{\omega_p}{\omega_s}\right),\frac{\omega_p}{\omega_s} \right)$$]Por la propiedad de simetría, se simplifica aún más. [$$ s_{cero\ m}=\frac{j \omega_s}{cd\left(\frac{2m+1}{n} K(\frac{\omega_p}{\omega_s}),\frac{\omega_p}{\omega_s} \right)}$$]
Para los ceros con los que nos quedamos en H(s), el valor de [$m$] se debe mover entre [$0$] y [$n-1$]. En algunos casos el cero aparecerá en el infinito. Eso significa que no debemos tenerlo en cuenta.
Para los polos hay que igualar [$\epsilon_p^2 R_n^2$] a menos uno. [$$ \epsilon_p^2 R_n^2 \left(\frac{\omega_{polo}}{\omega_p} , \frac{\omega_p}{\omega_s} ,\epsilon_p \epsilon_s \right)=-1$$][$$ R_n \left( \frac{\omega_{polo}}{\omega_p} , \frac{\omega_p}{\omega_s} ,\epsilon_p \epsilon_s \right) =\frac{j}{\epsilon_p}$$] Obtenemos una expresión similar a la que teníamos para los ceros. [$$ cd\left(n\ \frac{K(\epsilon_p \epsilon_s )}{K(\frac{\omega_p}{\omega_s})} arccd \left(\frac{-js_{polo}}{\omega_p} ,\frac{\omega_p}{\omega_s} \right),\epsilon_p \epsilon_s \right)=\frac{j}{\epsilon_p}$$]De nuevo elegimos el periodo real.[$$ n \frac{K(\epsilon_p \epsilon_s )}{K(\frac{\omega_p}{\omega_s})} arccd \left(\frac{-js_{polo\ m}}{\omega_p} ,\frac{\omega_p}{\omega_s}\right)=arccd\left(\frac{j}{\epsilon_p} ,\epsilon_p \epsilon_s \right)+2mK(\epsilon_p \epsilon_s )$$]Y despejamos[$$s_{polo\ m}=j \omega_p cd\left(\frac{K(\frac{\omega_p}{\omega_s})}{n\ K(\epsilon_p \epsilon_s ) } \left[arccd\left(\frac{j}{\epsilon_p} ,\epsilon_p \epsilon_s \right)+2mK(\epsilon_p \epsilon_s ) \right] ,\frac{\omega_p}{\omega_s}\right )$$]
Así podemos construir la magnitud de la función de transferencia al cuadrado a falta de la constante multiplicativa. [$$ |H(s) |^2=A^2 \frac{\prod{(s-s_{cero\ m})}}{\prod{(s-s_{polo\ m})}}$$] La constante se halla haciendo [$s=0$] en la expresión de [$|H(s) |^2$] basada en [$R_n^2$] e igualándola con la de arriba. [$$ |H(0) |^2=A^2 \frac{\prod{(0-s_{cero\ m})}}{\prod{(0-s_{polo\ m})}}=\frac{1}{1+\epsilon_p^2 R_n^2 (0,\frac{\omega_p}{\omega_s} ,\epsilon_p \epsilon_s ) }$$] Finalmente, se toman los polos con parte real menor que cero para conseguir que pueda ser realizado en la práctica.
Epílogo
Si el lector compara, para un mismo conjunto de especificaciones, los órdenes que se requieren de los filtros, verá que el filtro de Cauer mejora los otros dos tipos de filtros.
Debido a que el orden del filtro está relacionado con el número de componentes que se necesitan para hacer un circuito eléctrico del filtro, es inmediato llegar a la conclusión de que los filtros de Cauer son más económicos.
Esa es la razón por la que Cauer conseguía un filtro con las mismas prestaciones, pero con una bobina menos.
0 comentarios:
Publicar un comentario