Lo que nunca me enseñaron: Los filtros de Cauer (y parte IV)

Partes anteriores: 1, 2 y 3.

Las funciones elípticas de Jacobi

Las funciones elípticas de Jacobi son una generalización de las funciones trigonométricas. Hay doce funciones elípticas de Jacobi, pero sólo vamos a usar una que se llama [$cd$] y está relacionada con el coseno. Si bien el argumento de las funciones trigonométricas son ángulos, el argumento de las funciones elípticas de Jacobi es un valor [$u$] que no tiene una relación inmediata ni con los ángulos, ni áreas ni longitudes de arco.

Trigonometría en la elipse usando las funciones elípticas de Jacobi [$sd$], [$nd$] y [$cd$]. Hay más funciones elípticas de Jacobi, pero sólo nos será de utilidad la [$cd$].

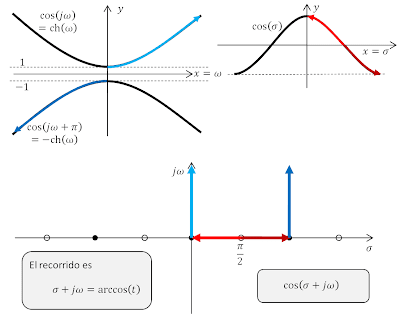
El valor [$k^'$] se llama el comódulo elíptico y se relaciona con la excentricidad de la elipse [$k$], también llamada el módulo elíptico, de la siguiente forma. [$$ k^2+(k^')^2=1$$] Dependiendo de la excentricidad de la elipse sobre la que trabajemos las funciones de Jacobi cambian por lo que es usual presentarlas con dos argumentos.[$$cd(u,k),\ \ \ \ sd(u,k),\ \ \ \ nd(u,k)$$] En concreto, la función [$cd(u,k)$] es muy parecida al coseno cuando se observa su inversa. [$$ arccd(u,k)=\int_u^1{\frac{dt}{\sqrt{1-t^2}\sqrt{1-k^2 t^2}}}$$] Investigaremos el recorrido que hace esta función cuando [$u$] se mueve desde [$0$] hasta infinito. Empieza en [$$ arccd(0,k)=\int_0^1{\frac{dt}{\sqrt{1-t^2} \sqrt{1-k^2 t^2}}}$$] Este valor es conocido como la integral elíptica completa de primera especie de módulo [$k$] y se escribe usualmente como [$K(k)$].

Diagrama representando el valor real resultado de la integral completa de primera especie que es el valor del [$arccd$] de cero.

Conforme aumente [$u$] por los reales, decrecerá el [$arccd$] hasta que lleguemos a [$u=1$] donde los límites de la integral van a coincidir por lo que su valor será cero. Si hacemos el recorrido simétrico hacia los valores negativos, llegaremos a [$u=-1$] donde el valor de su [$arccd$] será [$2K(k)$].

Recorrido del valor de [$arccd$] con argumentos desde cero hasta uno (y simétrico por los negativos).

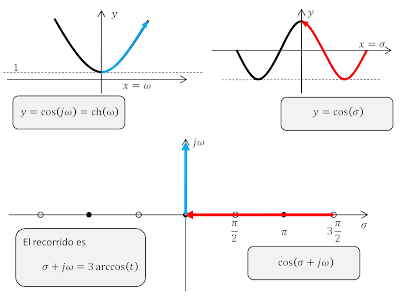
A partir de este punto, seguir integrando significa que la raíz [$\sqrt{1-t^2}$] va a resultar en valores imaginarios. Nuestro recorrido pasará a moverse verticalmente por la gráfica hasta que [$u=\frac{1}{k}$]. A partir de este valor, la raíz [$\sqrt{1-k^2 t^2}$] también se hace imaginaria. El valor del [$arccd$] en [$u=\frac{1}{k}$] es fácilmente calculable mediante un cambio de variables. [$$ arccd \left(\frac{1}{k},k\right)=\int_{\frac{1}{k}}^1{\frac{dt}{\sqrt{1-t^2}\sqrt{1-k^2 t^2}}}=\int_0^1{\frac{dt}{\sqrt{t^2-1}\sqrt{1-(k^')^2 t^2}}}=jK(k^' )$$] Trazando estos segmentos verticales del recorrido obtenemos el siguiente diagrama.

Recorrido del valor de [$arccd$] con argumentos desde cero hasta [$\frac{1}{k}$] (y simétrico por los negativos)

Finalmente, continuamos a partir de [$\frac{1}{k}$]. Ahora las dos raíces tienen el radicando negativo y son por tantos imaginarias, como [$j^2=-1$] el sentido de nuestro recorrido ha de ser opuesto al que inicialmente tenía. En el límite hacia el infinito será: [$$arccd(\infty,k)\rightarrow \int_\infty^1{\frac{dt}{\sqrt{1-t^2}\sqrt{1-k^2 t^2}}}=K(k)+jK(k^' )$$] Así que terminamos el recorrido de la siguiente manera.

Recorrido completo del valor de [$arccd$] con argumentos reales.

Sabiendo que al seguir este recorrido sobre la función [$cd(u,k)$] debemos obtener la función identidad, ganamos perspectiva de cómo es la función [$cd(u,k)$].

Secciones de cd

Su diagrama de polos y ceros se presenta a continuación y observamos que tiene dos periodos. El usual de [$4K(k)$] que se correspondería con el [$2\pi$] de las funciones trigonométricas y otro imaginario de [$2iK(k^' )$] que aparece por esa segunda raíz cuadrada en la integral. La zona sombreada es la que se repite periódicamente tanto horizontal como verticalmente.

Diagrama de polos, ceros y valores destacados de [$cd$].

Como hicimos con la función coseno, vamos a ver cómo es la función [$cd(u,k)$] en las tres secciones del recorrido de [$arccd(u,k)$]. Recordemos que en estas rectas la función [$cd(u,k)$] es real.

Tres secciones de la función [$cd$] por las rectas que va a seguir su [$arccd$]. En estas rectas el valor de [$cd$] es real y se representa a su derecha.

Para la rama negativa tenemos que [$$ cd(u+2K(k),k)=-cd(u,k)$$] Además, existe una propiedad de simetría entre [$cd(t,k)$] y [$cd(t+jK(k^' ),k)$] que usaremos más adelante. [$$cd(u+jK^' (k),k)=\frac{1}{k\ cd(u,k)}$$] En la DLMF podemos ver en 3D la función [$cd$] con sus polos bien distinguidos.

http://dlmf.nist.gov/22.3.F19.mag



La función racional elíptica


El lector astuto ya habrá imaginado que lo siguiente que vamos a hacer es [$$cd(n\ arccd(u ,k),k)$$] Como hicimos con los polinomios de Chebyshev, el recorrido del [$arccd$] queda ampliado [$n$] veces. Siguiéndolo, nos haremos una idea de cómo es esta función. Como antes, sólo seguiremos los valores positivos ya que los negativos son simétricos.

Recorrido de [$arccd$] ampliado tres veces sobre el diagrama de polos y ceros de [$cd$].

El resultado es una oscilación entre +1 y -1 en el primer segmento, otra oscilación entre 1 y 1/k en el segundo segmento y otra oscilación entre 1/k e infinito (cambiando de signo en cada infinito) en el tercer segmento.

Gráfica de la función [$cd(3\ arccd(x, k), k)$] con cada uno de los tramos coloreados.

Esta función no nos sirve como función [$F^2 (\omega)$] porque tendría oscilaciones en la banda de paso.

La función anterior al cuadrado como intento de aproximación a [$F^2(\omega)$]. La banda de transición es muy ancha y tiene oscilaciones.

Afortunadamente tenemos dos [$k$] a nuestra disposición, la del [$arccd$] que llamaremos [$k_a$] y la del [$cd$] que llamaremos [$k_c$]. Entonces, se define la función racional elíptica de la siguiente forma:[$$R_n (u,k_a,k_c )=cd\left(n\ \frac{K(k_c )}{K(k_a )} arccd(u ,k_a ),k_c \right)$$] La aparición del cociente [$\frac{K(k_c )}{K(k_a )}$] es necesaria para convertir el periodo real del [$arccd$] en el periodo real del [$cd$] que ahora son distintos al tener módulos distintos. Bueno, exactamente [$n$] veces ese periodo.
Por otra parte, ese n no lo queremos en el periodo imaginario. Querríamos tener [$$ R_n (u,k_a,k_c )=cd\left(\frac{K(k_c^' )}{K(k_a^' )} arccd(u ,k_a ),k_c \right)$$] ¡Y podemos tener ambas condiciones si elegimos con cuidado! [$$ n=\frac{K(k_a )K(k_c^' )}{K(k_a^' )K(k_c )} $$] De esta forma el recorrido queda multiplicado sólo en la dirección horizontal.

El recorrido que tomamos en la función elíptica racional con unos parámetros adecuados para que sólo se mueva medio periodo imaginario.

La gráfica de esta función es como sigue. En ella aparece tanto la [$k_a$] como la [$k_c$] explícitamente.

Gráfica de la función elíptica racional con módulos [$k_a$] y [$k_c$] (y la [$n$] adecuada según se comentó arriba).

Como ocurría con los polinomios de Chebyshev, esta función es real, aunque esta vez no puede expresarse como un polinomio ya que tiene polos (los infinitos). Debe expresarse como un cociente entre polinomios, de ahí que se llame función racional elíptica.

El filtro de Cauer

El filtro de Cauer o filtro elíptico es el que toma esa función racional elíptica como [$F(\omega)$]. La gráfica de su cuadrado es la que sigue.

La función racional elíptica como función [$F(\omega)$] de un filtro.

Ajustando para que se cumplan los requisitos de un filtro tenemos que [$$ F^2 (\omega)=\epsilon_p^2 R_n^2 \left(\frac{\omega}{\omega_p} ,\frac{\omega_p}{\omega_s} ,\epsilon_p \epsilon_s \right)$$] Donde hemos usado [$$k_a=\frac{\omega_p}{\omega_s}$$][$$ k_c=\epsilon_p \epsilon_s$$]

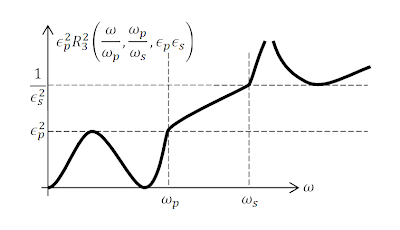La función racional elíptica como función   [$F(\omega)$] de un filtro con los parámetros ajustados a las especificaciones del filtro.  

Así que un filtro de Cauer de orden [$n$] tiene la siguiente respuesta en frecuencia al cuadrado. [$$ |H(j\omega) |^2=\frac{1}{1+\epsilon_p^2 R_n^2 \left( \frac{\omega}{\omega_p} ,\frac{\omega_p}{\omega_s} ,\epsilon_p \epsilon_s \right)}$$] Realmente, su banda de transición es mucho más pequeña que lo trazado en las gráficas anteriores. La siguiente gráfica muestra la respuesta en frecuencia bien escalada.

Respuesta en frecuencia de un filtro de Cauer

Además, la condición de la no oscilación en la banda base y ajuste de periodos es precisamente la cota del orden del filtro. [$$ n\ge \frac{K(\frac{\omega_p}{\omega_s}) K^' (\epsilon_p \epsilon_s )}{K^' ( \frac{\omega_p}{\omega_s} )K( \epsilon_p \epsilon_s )}$$] Donde [$K^' (k)=K(k^' )$].
Ojo: una vez hallado [$n$] con la desigualdad, hemos de modificar algún requisito para que se cumpla la igualdad. Debemos tener la igualdad si no queremos oscilaciones en la banda de transición.

La búsqueda de la función de transferencia

Para obtener la función de transferencia necesitamos conocer los polos y los ceros de la misma. Ambos son sencillos de calcular. Hagamos el cambio [$\omega=-js$] y empecemos por los ceros de la función de transferencia. Ocurrirán cuando [$R_n^2$] tienda a infinito. Es decir, en los polos de [$R_n^2$]. [$$R_n^2 \left(\frac{-js_{cero}}{\omega_p} ,\frac{\omega_p}{\omega_s} ,\epsilon_p \epsilon_s \right)=\infty$$] [$$n \frac{K(\epsilon_p \epsilon_s )}{K(\frac{\omega_p}{\omega_s} )} arccd\left(\frac{-js_{cero}}{\omega_p} ,\frac{\omega_p}{\omega_s} \right)=arccd(\infty,\epsilon_p \epsilon_s )$$]
El miembro de la derecha es la localización de los polos de [$cd$]. Recordemos que hay dos periodos y, por la dirección del recorrido del [$arccd$] en la zona de los ceros, nos interesa el periodo real.[$$n \frac{K(\epsilon_p \epsilon_s )}{K(\frac{\omega_p}{\omega_s})} arccd\left(\frac{-js_{cero\ m}}{\omega_p} ,\frac{\omega_p}{\omega_s}\right)=(2m+1)K(\epsilon_p \epsilon_s )+jK^' (\epsilon_p \epsilon_s )$$]
Despejando llegamos a la expresión siguiente. [$$ s_{cero\ m}=j\omega_p cd\left(\frac{2m+1}{n} K\left(\frac{\omega_p}{\omega_s}\right)+jK^' \left(\frac{\omega_p}{\omega_s}\right),\frac{\omega_p}{\omega_s} \right)$$]Por la propiedad de simetría, se simplifica aún más. [$$ s_{cero\ m}=\frac{j \omega_s}{cd\left(\frac{2m+1}{n} K(\frac{\omega_p}{\omega_s}),\frac{\omega_p}{\omega_s} \right)}$$]
Para los ceros con los que nos quedamos en H(s), el valor de [$m$] se debe mover entre [$0$] y [$n-1$]. En algunos casos el cero aparecerá en el infinito. Eso significa que no debemos tenerlo en cuenta.
Para los polos hay que igualar [$\epsilon_p^2 R_n^2$] a menos uno. [$$ \epsilon_p^2 R_n^2 \left(\frac{\omega_{polo}}{\omega_p} , \frac{\omega_p}{\omega_s} ,\epsilon_p \epsilon_s \right)=-1$$][$$ R_n \left( \frac{\omega_{polo}}{\omega_p} , \frac{\omega_p}{\omega_s} ,\epsilon_p \epsilon_s \right)  =\frac{j}{\epsilon_p}$$] Obtenemos una expresión similar a la que teníamos para los ceros. [$$ cd\left(n\ \frac{K(\epsilon_p \epsilon_s )}{K(\frac{\omega_p}{\omega_s})} arccd \left(\frac{-js_{polo}}{\omega_p} ,\frac{\omega_p}{\omega_s} \right),\epsilon_p \epsilon_s \right)=\frac{j}{\epsilon_p}$$]De nuevo elegimos el periodo real.[$$ n \frac{K(\epsilon_p \epsilon_s )}{K(\frac{\omega_p}{\omega_s})} arccd \left(\frac{-js_{polo\ m}}{\omega_p} ,\frac{\omega_p}{\omega_s}\right)=arccd\left(\frac{j}{\epsilon_p} ,\epsilon_p \epsilon_s \right)+2mK(\epsilon_p \epsilon_s )$$]Y despejamos[$$s_{polo\ m}=j \omega_p cd\left(\frac{K(\frac{\omega_p}{\omega_s})}{n\ K(\epsilon_p \epsilon_s ) } \left[arccd\left(\frac{j}{\epsilon_p} ,\epsilon_p \epsilon_s \right)+2mK(\epsilon_p \epsilon_s ) \right] ,\frac{\omega_p}{\omega_s}\right )$$]
Así podemos construir la magnitud de la función de transferencia al cuadrado a falta de la constante multiplicativa. [$$ |H(s) |^2=A^2 \frac{\prod{(s-s_{cero\ m})}}{\prod{(s-s_{polo\ m})}}$$] La constante se halla haciendo [$s=0$] en la expresión de [$|H(s) |^2$] basada en [$R_n^2$] e igualándola con la de arriba. [$$ |H(0) |^2=A^2 \frac{\prod{(0-s_{cero\ m})}}{\prod{(0-s_{polo\ m})}}=\frac{1}{1+\epsilon_p^2 R_n^2 (0,\frac{\omega_p}{\omega_s} ,\epsilon_p \epsilon_s ) }$$] Finalmente, se toman los polos con parte real menor que cero para conseguir que pueda ser realizado en la práctica.

Epílogo

Si el lector compara, para un mismo conjunto de especificaciones, los órdenes que se requieren de los filtros, verá que el filtro de Cauer mejora los otros dos tipos de filtros.

Debido a que el orden del filtro está relacionado con el número de componentes que se necesitan para hacer un circuito eléctrico del filtro, es inmediato llegar a la conclusión de que los filtros de Cauer son más económicos.

Esa es la razón por la que Cauer conseguía un filtro con las mismas prestaciones, pero con una bobina menos.

Lo que nunca me enseñaron: Los filtros de Cauer (parte III)

La primera parte está aquí y la segunda parte aquí.

Los viajes del arcocoseno

Hasta aquí todo lo visto ha sido para entender el proceso de realización de un filtro. A partir de aquí empezamos a acercarnos a los filtros elípticos. Sin embargo, antes debemos pararnos a explorar los filtros de Chebyshev. Los filtros de Chebyshev son más simples porque usan para su expresión matemática la circunferencia en vez de la elipse. Deberían llamarse filtros circulares, pero ya se ha quedado el nombre de Chebyshev.

Lo primero que necesitamos para entender los filtros de Chebyshev es la definición de arcocoseno. [$$arccos(x)=\int_x^1{\frac{dt}{\sqrt{1-t^2}}}$$] Esta integral no es más que la longitud de arco de una circunferencia unitaria desde una abscisa [$x$]. (Nota: Por supuesto, es una función multivaluada. Tomaremos sólo la rama de la raíz principal aquí).

El arcocoseno no es más que la longitud del arco marcado.

Lo sorprendente es que esta integral, el arcocoseno, tiene sentido cuando [$x$] va más allá de [$\pm 1$]. Eso sí, hemos de usar números complejos porque el radicando que aparece en la raíz se hace negativo.
Dibujaremos el valor que toma el arcocoseno en el plano de Argand conforme [$x$] tome valores reales. Empezaremos por el arcocoseno de cero que es [$\pi/2$].

El arcocoseno de cero es [$\pi/2$].

Si vamos aumentando [$x$], llegamos hasta [$arccos(1)=0$] obteniendo únicamente números reales. Es el arcocoseno clásico. Igualmente, si disminuimos [$x$], llegamos hasta [$arccos(-1)=\pi$]. Esta simetría continuará por lo que no hablaremos más de los valores negativos de [$x$].

El recorrido desde el arcocoseno de cero al arcocoseno de uno (y menos uno).

En el punto [$arccos(1)=0$] ocurre que la raíz del integrando se anula. [$$\sqrt{1-t^2 }=0$$] Si seguimos moviendo [$x$] por la recta real, el arcocoseno entrará en el eje imaginario. A partir de aquí tenemos otras dos ramas, la raíz positiva y la negativa. Elegimos la positiva y recordamos para luego que hay simetrías.

El recorrido del valor del arcoseno de los números reales.

Las olas del coseno

En los complejos, el coseno es una función holomorfa. Una de sus particularidades es la periodicidad en el eje real. Si trazamos su diagrama de ceros (no tiene polos) y añadimos algunos puntos destacados en la línea real obtenemos lo siguiente.

Los valores destacados que toma el coseno cuando su argumento es un número complejo.

Si recorremos el plano de Argand por la línea real [$x=\sigma$], obtenemos la función coseno clásica. El lado más oscuro corresponde a los valores negativos.

Los valores del coseno cuando su argumento es un número real ([$\omega=0$])

Si recorremos el coseno por la recta imaginaria obtenemos el coseno hiperbólico. Es importante darse cuenta que por estos dos recorridos el coseno siempre proporciona un valor real.

Los valores del coseno cuando su argumento es un número imaginario ([$\sigma=0$])

Como era de esperar, al ser el arcocoseno la función inversa del coseno, si hacemos el recorrido del arcocoseno desde 0 hasta infinito, vamos visitando los argumentos cuyo coseno se mueve desde 0 hasta infinito.

Los valores del arcocoseno recorren los argumentos del coseno cuyo resultado es el argumento del arcocoseno. Son funciones inversas una de otra.

Los polinomios de Chebyshev

Los polinomios de Chebyshev se definen así: [$$C_n (x)=cos(n\ arccos(x) )$$] Para ver cómo son, observemos el recorrido de [$n\ arccos(x)$] sobre la función coseno. Es muy sencillo porque lo único que hacemos al multiplicar por [$n$] es ampliar fotográficamente [$n$] veces el recorrido del arcocoseno. En el siguiente diagrama usamos [$n=3$].

El polinomio de Chebyshev de orden tres se obtiene ampliando por tres el recorrido del arcocoseno (la gráfica de abajo) y, luego, realizar el coseno (las dos gráficas de arriba).

Ampliar tres veces el recorrido no cambia mucho el valor del coseno por la recta imaginaria. Lo hace más abrupto porque nos movemos más rápidamente hacia el infinito. En donde sí que hay un cambio es en la parte real donde tenemos tres cuartos de pi en vez de uno. Esto hace que se oscile en esa parte.

Recordemos que en estas rectas todos los valores del coseno son reales y que hay otra parte simétrica cuando [$t\lt 0$]. Con esto en mente podemos dibujar [$C_3$].

Polinomio de Chebyshev de orden tres.

Observando con cuidado el recorrido de arriba, vemos que atraviesa exactamente 3 ceros del coseno: el [$\pi/2$] y su simétrico en [$5 \pi/2$] y el [$3 \pi/2$] que es su propio simétrico. Además, no es casual que los puntos donde [$x=\pm 1$] tome el valor [$y= \pm 1$] ya que son los puntos de arcocoseno nulo.

Una manera fácil de calcular los polinomios de Chebyshev es la siguiente. [$$C_{n+1} (x)=cos(n\ arccos(x)+arccos(x) )=x C_n (x)+sin(n\ arccos(x) ) sin(arccos (x) )$$][$$ C_{n-1}(x)=cos(n\ arccos(x)-arccos(x) )=x C_n (x)-sin(n\ arccos(x) ) sin(arccos(x) )$$] Sumando se llega a [$C_{n+1} (x)+C_{n-1} (x)=2 x C_n (x)$] y despejando [$C_{n+1} (x)$] se obtiene la siguiente fórmula recursiva. [$$C_{n+1} (x)=2 C_n (x) - C_{n-1} (x)$$] Usando la definición se obtiene que [$C_0 (x)=1$] y [$C_1 (x)=x$] con lo que tenemos todos los datos para calcular el polinomio de Chebyshev del orden que queramos.

El filtro de Chebyshev

La función [$C_n^2 (\omega)$] es una buena aproximación de [$F^2 (\omega)$]. Dibujemos su gráfica para n=3.

El polinomio de Chebyshev de tercer grado al cuadrado como aproximación a [$F^2(\omega)$].

Para que cumpla los requisitos de un filtro hay que ajustarla un poco. [$$ F^2 (\omega)=\epsilon_p^2 C_n^2 \left(\frac{\omega}{\omega_p} \right)$$]

La función [$F^2(\omega)$] de un filtro de Chebyshev.

Así que un filtro de Chebyshev es el que tiene la siguiente respuesta en frecuencia al cuadrado. [$$ |H(j\omega) |^2=\frac{1}{1+\epsilon_p^2 C_n^2 \left(\frac{\omega}{\omega_p} \right)}$$] A partir de aquí procedemos como en el filtro de Butterworth. Calculamos [$\epsilon_s$], despejamos [$n$] para el orden; calculamos los polos de [$|H(s) |^2$] (este filtro no tiene ceros) y separamos los polos para obtener [$H(s)$].

Todo esto lo dejaremos para el lector que observará, entre otras cosas, que el orden requerido es menor en un filtro de Chebyshev que en un filtro de Butterworth para los mismos requisitos.

El lector curioso queda emplazado para explorar los filtros inversos de Chebyshev e intentar usar la misma técnica de inversión para los filtros de Butterworth.

Continúa y acaba en la cuarta parte.

Lo que nunca me enseñaron: Los filtros de Cauer (parte II)

Parte 1 aquí.

El filtro de Butterworth

Aproximar la función [$F^2 (\omega)$] que debería valer 0 si [$\omega < \omega_p$] e infinito si [$\omega > \omega_s$] es muy sencillo. Todas las funciones monótonas (siempre crecientes) lo aproximan con más o menos éxito.

Una [$F^2 (\omega)$] muy usada es [$$F^2 (\omega)=  \epsilon  _p^2 \left(\frac{ \omega }{  \omega_p } \right)^{2n}$$] Este es el llamado filtro de Butterwoth. El número [$n$] es el orden del filtro. Debido a que debemos trabajar con polinomios, las potencias han de ser números naturales y, por tanto, el orden del filtro n debe ser un número natural. El orden del filtro está relacionado con el número de componentes eléctricos que va a tener nuestro circuito.

Construyamos su respuesta en frecuencia al cuadrado. [$$ |H(j\omega)|^2=\frac{1}{1+\epsilon_p^2 \left(\omega/\omega_p \right)^{2n}}$$] El filtrado de frecuencias que hace este filtro se muestra a continuación. Esta gráfica es la original del artículo de Butterworth de 1930 y representa [$|H(j\omega)|$] con [$\omega_p=1$].

Respuesta en frecuencia de un filtro de Butterworth tal cual aparecía en su artículo de 1930.

El valor [$\epsilon_p$] está explícitamente escrito en la ecuación, pero no sabemos nada de [$\epsilon_s$]. Hemos de usar la expresión de [$|H(j\omega) |^2$] para deducir qué valor tendremos para [$\epsilon_s$]. Bastará calcular la respuesta en frecuencia a la frecuencia [$\omega_s$]. [$$|H(j\omega_s ) |^2=\frac{1}{1+\epsilon_p^2 \left(\omega_s/\omega_p\right)^{2n}} = \frac{\epsilon_s^2}{1+\epsilon_s^2}$$][$$ \frac{1}{\epsilon_s^2}=\epsilon_p^2 \left(\frac{\omega_s}{\omega_p}\right)^{2n},\ \ \ \ \epsilon_s \epsilon_p=\left( \frac{\omega_p}{\omega_s}\right) ^n$$] Esta última expresión, muy simple gracias a la introducción de los épsilon en la parte anterior, relaciona el orden del filtro con los requisitos. Como el orden del filtro ha de ser un natural, es usual escribir la ecuación como una cota. [$$ n \ge \frac{log(\epsilon_s \epsilon_p)}{log \left( \frac{\omega_p}{\omega_s} \right) } $$]

Polos y ceros

La función [$|H(j\omega) |^2$] está relacionada con la respuesta en frecuencia del filtro [$|H(j\omega) |$] sin cuadrado, pero lo que nos interesa para poder implementar el filtro es la función de transferencia [$H(s)$] que abarca todos los complejos. Los pasos son los siguientes.

Primero, con un cambio de variables [$\omega=-js$], convertimos [$|H(j\omega) |^2$] en [$|H(s) |^2$].  [$$ |H(s)|^2=\frac{1}{1+\epsilon_p^2 \left(-js/\omega_p \right)^{2n}}$$]
A continuación, obtendremos la función [$|H(s) |^2$] como un cociente de dos polinomios. Escribiremos los polinomios factorizando sus raíces. [$$|H(s) |^2=A^2 \frac{\prod{s-s_{cero m} }}{\prod{s-s_{polo m} }}$$] Las raíces del numerador se llaman ceros porque cuando [$s$] sea un [$s_{cero}$], tendremos que [$|H(s) |^2=0$]. Las raíces del denominador se llaman polos porque cuando [$s$] tienda a un [$s_{polo}$], todo [$|H(s) |^2$] tiende a infinito. El por qué se llaman polos es obvio cuando se hace la gráfica en tres dimensiones.

Visión 3D de la función de transferencia de un filtro de Butterworth. Se observan los polos y la respuesta en frecuencia cuya parte positiva está remarcada en rojo.

Los filtros de Butterworth no tienen ceros. Esto ocurre porque el numerador de [$|H(s) |^2$] es uno. Pero sí tienen polos cuando el denominador se anula. Es decir, cuando [$F^2 (\omega)=-1$].[$$F^2 (-js_{polo} )=-1$$][$$\epsilon_p^2 \left(\frac{-js_{polo}}{\omega_p}\right)^{2n}=-1$$][$$\epsilon_p \left(\frac{-js_{polo}}{\omega_p}\right)^n=j$$][$$  \sqrt[n]{\epsilon_p}\frac{-js_{polo}}{\omega_p}=\sqrt[n]{j}$$][$$s_{polo}=\frac{j \omega_p}{\sqrt[n]{\epsilon_p}} \sqrt[n]{j}$$]
Usando las raíces de la unidad, llegamos a que los polos de [$|H(s) |^2$] yacen en un círculo. Como hay más de uno, los numeramos con un subíndice [$m$]. [$$s_{polo\ m}=\omega_p \epsilon_p^{\frac{-1}{n}} e^{j\left[\frac{p}{2}+\frac{p}{2n}+\frac{2p}{n} m\right]}$$] Es interesante localizar los polos en el plano de Argand (plano complejo). El siguiente diagrama muestra los polos de [$|H(s) |^2$] de un filtro de Butterworth de orden tres.

Distribución de los polos de la función de transferencia al cuadrado de un filtro de Butterworth de orden tres.

Obteniendo la función de transferencia

La simetría que aparece en el diagrama anterior es usual en [$|H(s) |^2$] y se llama simetría cuadrantal. Ocurre que [$$|H(s) |^2=|H(-s) |^2=|H(s^* ) |^2$$] por lo que la función [$|H(s) |^2$] queda completamente definida por lo que pase en sólo uno de sus cuadrantes. Esta simetría se usa para obtener [$H(s)$] a partir de [$|H(s) |^2$] mediante la siguiente ecuación: [$$|H(s) |^2=H(s)H(-s)$$] Recordemos que [$|H(s) |^2$] estaba descrita como un producto de polos y ceros. Entonces, podemos separar los polos que van para [$H(s)$] y los que van para [$H(-s)$].[$$ A^2 \frac{\prod{(s-s_{cero\ m})}}{\prod{(s-s_{polo\ m})}}=\left[A \frac{\prod{(s-s_{cero\ de\ H(s)\ m})}}{\prod{(s-s_{polo\ de\ H(s)\ m} )}}\right]\left[A \frac{\prod{(s-s_{cero\ de\ H(-s)\ m} )} }{\prod{(s-s_{polo\ de\ H(-s)\ m}) } }\right]$$] Lo que sí que hay que decidir es qué polos van para [$H(s)$] y qué polos van para [$H(-s)$]. Es fácil. Para que [$H(s)$] sea realizable físicamente y estable, hay que escoger los polos cuya parte real sea negativa. Y para que el filtro sea de fase mínima (menor dispersión) también cogeremos los ceros que tengan su parte real negativa.

Separación de los polos de [$|H(s)|^2$] que van para [$H(s)$] de los que van para [$H(-s)$].

Una vez tenemos [$H(s)$] podemos usar alguna de las técnicas de síntesis de circuitos para realizar el filtro.

Continúa en la parte tres.

Lo que nunca me enseñaron: Los filtros de Cauer (parte I)

Introducción

Según cuenta Van Valkenburg (ver "Analog Filter Design" 1982, página 379), sobre 1935 los ingenieros de Bell Laboratories se llevaron una desagradable sorpresa. Su competencia alemana había sacado un teléfono al mercado que igualaba la calidad de sonido del suyo, pero usaba un inductor menos en los filtros.
En 1935 los inductores no eran lo que hoy. Un inductor pesaba su cuarto de kilo y costaba bastante. El que los alemanes hubieran conseguido eliminarlo sin deteriorar las características del dispositivo podría llevar la empresa americana a la ruina y no era época para tonterías con los alemanes.

Teléfono de 1930

Pero esa ruina no ocurrió. El inventor del método de diseño que hacía capaz ese ahorro, Wilhelm Cauer, estaba necesitado de dinero (supongo) y quiso vender sus patentes. Para eso dio unas conferencias y los muy avispados matemáticos de Bell Laboratories tomaron nota. Una familia de funciones matemáticas se mencionó varias veces: las funciones elípticas de Jacobi.

Cuenta la leyenda que durante las dos semanas siguientes el departamento entero de matemáticas de Bell Laboratories se encerró en la biblioteca pública de Nueva York, estudiando tales funciones. Si mal no recuerda Darlington, que lo sufrió en sus propias carnes, allí encontró el artículo original de Jacobi de 1829 escrito en latín. En él estaba todo: tablas, transformaciones, aproximaciones… ¡todo!

A fin de cuentas, Cauer fue estudiante de Hilbert en Göttingen. Dada la prominencia del maestro, seguramente había visto de sobra estas funciones elípticas y, simplemente, les había encontrado otra aplicación. Por ese motivo, a este tipo de filtros se los denomina filtros elípticos o filtros de Cauer.

David Hilbert y Wilhelm Cauer

Los filtros

Un filtro eléctrico no es más que un dispositivo que toma una señal eléctrica como la del teléfono y elimina algunas frecuencias. De esta manera podemos oír la voz sin los ruidos raros del ADSL introduciendo un filtro que elimine las frecuencias que usa el ADSL. Lógicamente, podremos usar otro filtro para quedarnos con el ADSL y quitar la voz. Así que, por un mismo cable y gracias a un par de filtros, tengo voz y datos.

Splitter de ADSL que no es más que un filtro para que no se oiga el ruido de los datos de ADSL en el audio del teléfono.

Esta no es más que una de las aplicaciones de los filtros. Hay muchísimas más: multiplexar, eliminar el aliasing, hacer efectos de sonido y ecualizar, compensar desfases, modular, demodular… y un sinfín más que no vamos a enumerar aquí porque lo que nos interesa es el trasfondo teórico de los filtros.

La función de transferencia y la respuesta en frecuencia

La forma que tienen los filtros de procesar las señales es mediante una función de transferencia [$H(s)$]. Esta función está definida en los números complejos y, para que pueda ser construida físicamente, ha de ser racional (P y Q son polinomios). [$$H(s)=\frac{P(s)}{Q(s)}$$] La magnitud de la función de transferencia en el eje imaginario es la respuesta en frecuencia. Esta respuesta es lo que nuestro filtro multiplicará a la amplitud cada frecuencia. Si su valor a una frecuencia es mayor que uno, esa frecuencia se amplifica. Si es menor que uno, se atenúa. Escribiremos esta magnitud así:[$$|H(j\omega)|$$] Donde [$\omega$] no es más que [$2\pi$] veces la frecuencia ([$\omega=2\pi f$]) para no tener que escribir [$2\pi$] cada vez que vayamos a usar un seno, coseno o exponencial compleja. La [$j$] es la constante imaginaria que, en ingeniería, se usa para no confundirla con la intensidad de corriente [$i$].

Es importante señalar aquí que para realizar el filtro necesitamos la función [$H(s)$] con [$s$] en todo el plano complejo, pero la respuesta en frecuencia que deseamos es sólo esa función en la recta imaginaria [$|H(j\omega)|\ \ $]. Gran parte del problema estriba en pasar de [$|H(j\omega)|\ \ $], lo que queremos, a [$H(s)$], cómo hacerlo.

Pero primero veamos qué queremos.

El filtro ideal y los filtros reales

Nos interesaría que la respuesta en frecuencia fuera ideal: todo lo que haya por encima de una frecuencia de corte [$\omega_c$] se elimina (se multiplica por 0 en la banda de rechazo) y todo lo que haya por debajo se preserva (se multiplica por 1 en la banda de paso). Eso significa que el [$|H(j\omega)|$] ideal tendría esta forma:

Un filtro ideal que elimina las frecuencias de la banda de rechazo y deja intactas las frecuencias de la banda de paso.

Sin embargo, esto no es posible porque las únicas funciones de transferencia que podemos realizar eléctricamente son funciones racionales (recordemos: cocientes de dos polinomios) y son funciones continuas excepto en asíntotas verticales. No es posible hacer el escalón discontinuo que vemos en la gráfica de arriba. Hay que transigir y permitir no tener exactamente un 1 o un 0 (a esto se le denomina rizado) y dejar una banda de transición entre las bandas de paso y de rechazo.

Forma de un filtro real donde se han especificado los requisitos del mismo: frecuencia de paso [$\omega_p$], frecuencia de rechazo [$\omega_s$], rizado de paso [$r_p$] y rizado de rechazo [$r_s$].

Ya no tenemos una frecuencia de corte, sino una frecuencia de paso [$\omega_p$] por debajo de la cual las frecuencias no se van a tocar mucho (entre [$1$] y [$r_p$]) y una frecuencia de rechazo [$\omega_s$] por encima de la cual no van a sobrevivir muchas frecuencias (como mucho se multiplica por [$r_s$] que será todo lo cercano a cero posible).

Nota: El subíndice s viene del inglés stopband.

Complicando para simplificar

Como vemos, todo el rango de trabajo está entre el [$0$] y el [$1$]. Si elevamos al cuadrado, seguimos estando entre [$0$] y [$1$]. Esto permite trabajar con la magnitud al cuadrado que es más sencilla de calcular y siempre es real positiva. [$$ |H(j\omega)|^2=H(j\omega) H^*(j\omega)=H(j \omega )H(-j \omega )$$] El asterisco indica complejo conjugado. La última igualdad saca provecho a que [$H(s)$] es racional con coeficientes reales y, por tanto, su parte imaginaria ha de ser hermítica.

Trabajar entre [$0$] e infinito es también más sencillo. ¿Por qué? Si el límite es el [$1$], nos podemos pasar de [$1$] y eso sería erróneo. Nos tendríamos que dedicar a comprobar que nuestros cálculos nunca superasen el uno y los complicaría. En cambio, si el límite es infinito, ¡no hay límite! Los cálculos no tienen necesidad de asegurar que haya un límite y se simplifican.

Forzaremos que la función [$|H(j\omega)|^2$] tenga esta forma: [$$ |H(j\omega)|^2=\frac{1}{1+F^2 ( \omega )}$$]Ahora, la función [$F^2 ( \omega )$] no tiene límite superior. A cambio, hemos de recalcular los rizados.

La misma respuesta en frecuencia de antes, pero con la transformación mencionada para trabajar entre [$0$] e infinito. Hay que hacer notar cómo se han modificado los parámetros que especificaban los rizados.

Estos nuevos parámetros [$\epsilon_s$] y [$\epsilon_p$] se relacionan con los rizados originales así: [$$r_p=\sqrt{\frac{1}{1+\epsilon_p^2}},\ \ \ \ r_s=\sqrt{\frac{\epsilon_s^2}{1+ \epsilon _s^2}}$$] Llamaremos a [$\omega_p,\epsilon_p,\omega_s$] y [$\epsilon_s$] los requisitos del filtro.

Hay que destacar que la función [$F^2 (\omega)$] sigue siendo una función racional y deberá ser el cociente de dos polinomios.

Continúa en parte dos.

miniSL parte 14 - La Evaluación

Retomamos el lenguaje de script miniSL. Hasta ahora hemos definido los datos sobre los que vamos a tratar (las celdas) y hemos implementado las operaciones básicas sobre ellos: creación y destrucción. También hemos destacado algunos datos como el entorno global.

Ahora vamos a implementar la principal operación a realizar sobre los datos: tomar una celda que represente una expresión y calcular su valor (que será otra celda). Esto es lo que se llama la evaluación.

Existen varios modelos de evaluación. Aquí nos centraremos en la evaluación por entornos (se explica aquí y aquí). Este tipo de evaluación es realmente sencilla: si queremos saber el valor de una variable, hemos de buscarla en el entorno actual. Si no, buscamos en el entorno padre y así sucesivamente. Esto lo hace la función FindName() que se vio en la parte 10.

La evaluación de literales es inmediata: representan su propio valor (el 5 es el 5, la cadena “hola” es la cadena “hola”). La evaluación de combinaciones (aplicaciones de una función a argumentos) procede de la siguiente manera.

1. Se evalúa el operador (la función).
2. Se envían los operandos sin evaluar a la función.

Como hay dos tipos de funciones: la definida por el usuario y la nativa, tendremos que contemplar ambos casos. En principio, la definida por el usuario evaluará los operandos; pero veremos que las nativas necesitan sus operandos sin evaluar (en las partes 29,30 y siguientes).

La evaluación de una lista es la lista de sus miembros evaluados. Así, [1+2,5] es la lista [3,5]. La lista vacía es precisamente un literal porque no hay que evaluar nada para calcular su valor.

Cualquier otra celda no es considerada expresión y genera un error de ejecución.

El código de la función de evaluación es el siguiente:

CELL& Script::Evaluate(CELL& c, CELL& envir)
{
 CELL* aux;
 switch(c.type)
 {
  //Non evaluable
 case UNUSED: throw L"Evaluating an unused cell";
 default:  throw L"Evaluating an unknown cell";
 case LAMBDA_VAL:throw L"Evaluating a lambda value";
 case NATIVE_VAL:throw L"Evaluating a native";
 case ENVIR_VAL: throw L"Evaluating an environment";

  //Literals
 case INT_LIT: case BOOL_VAL: case STRING_LIT: case EMPTY_LIT:
  return c;

  //Code constructors
 case CONS_CTOR:  return CreateCell(CONS_CTOR, &Evaluate(*c.head, envir), &Evaluate(*c.tail, envir));

 case NAME_CODE: 
  if((aux=FindName(c, envir))==NULL)
   throw L"Unknown name";
  return *aux;

 case COMBINE_CODE:
  switch((aux=&Evaluate(*c.op, envir))->type)
  {
  case LAMBDA_VAL: return ApplyLambda(*aux->code, *c.operands, *aux->closure, envir);
  case NATIVE_VAL: return aux->native(*this, *c.operands, envir);
  default:   throw L"Non-combinable value";
  }
 }
}

Lo más complejo es la evaluación de la combinación. Esto es debido a los casos antes mencionados. Cuando tenemos una operación nativa, directamente llamamos a la función que la implementa. Si tenemos una operación definida por el usuario (lambda) usaremos una función auxiliar ApplyLambda() que veremos en la siguiente parte de esta serie.